
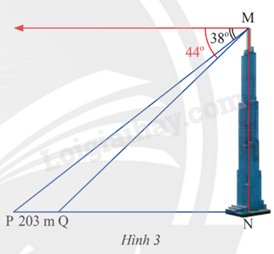
Hai điểm P và Q cách nhau 203 m và thẳng hàng với chân một tòa tháp (Hình 3). Từ đỉnh của tòa tháp đó, một người nhìn thấy hai điểm P, Q với hai góc nghiêng xuống lần lượt là \({38^o}\) và \({44^o}\). Tính chiều cao của tòa tháp (kết quả làm tròn đến hàng đơn vị của mét).

- Tìm \(\widehat {QMN}\) và \(\widehat {PMN}\)
- Dựa vào định lí: Xét tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông còn lại nhân tang góc đối hoặc nhân côtang góc kề rồi suy ra cạnh góc vuông.
- Từ đó lập biểu thức PN – QN = 203 để tính MN.

Ta có: \(\widehat {QMN} = {90^o} - {44^o} = {46^o}\), \(\widehat {PMN} = {90^o} - {38^o} = {52^o}\)
Advertisements (Quảng cáo)
Xét tam giác MQN vuông tại N, ta có:
QN = MN. tan\(\widehat {QMN}\)
Xét tam giác MPN vuông tại N, ta có:
PN = MN. tan\(\widehat {PMN}\)
Mặt khác, ta có PN – QN = 203
Suy ra MN. tan\(\widehat {PMN}\) - MN. tan\(\widehat {QMN}\) = 203
MN.( tan\(\widehat {PMN}\) - tan\(\widehat {QMN}\)) = 203
Vậy MN = \(\frac{{203}}{{\tan \widehat {PMN} - \tan \widehat {QMN}}} = \frac{{203}}{{\tan {{52}^o} - \tan {{46}^o}}} = 830,6\)
Vậy chiều cao của toàn tháp là 830,6 m.
