Giải mục 3 trang 40 Toán 9 Chân trời sáng tạo tập 1: Nếu chân thang cách chân tường x (m) thì đỉnh thang ở độ cao bao nhiêu so với chân...

Hoạt động2

Trả lời câu hỏi Hoạt động 2 trang 40

Một chiếc thang dài 5m tựa vào bức tường như Hình 3.

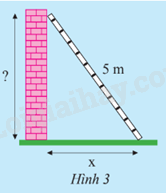
a) Nếu chân thang cách chân tường x (m) thì đỉnh thang ở độ cao bao nhiêu so với chân tường?

b) Tính độ cao trên khi x nhận giá trị lần lượt là 1;2;3;4.

Áp dụng định lý Pythagore vào tam giác vuông tạo bởi chiếc thang và bức tường.

Thay lần lượt từng giá trị x để tính độ cao.

a) Đỉnh thang có độ cao là: \(\sqrt {{5^2} - {x^2}} \) (m).

b) Khi x = 1 thì độ cao là \(\sqrt {{5^2} - {1^2}} = 2\sqrt 6 \) (m)

Khi x = 2 thì độ cao là \(\sqrt {{5^2} - {2^2}} = \sqrt {21} \)(m)

Khi x = 3 thì độ cao là \(\sqrt {{5^2} - {3^2}} = 4\)(m)

Khi x = 4 thì độ cao là \(\sqrt {{5^2} - {4^2}} = 3\)(m)

Thực hành7

Trả lời câu hỏi Thực hành 7 trang 40

Với giá trị nào của x thì biểu thức A = \(\sqrt {3x + 6} \) xác định? Tính giá trị của A khi x = 5 (kết quả làm tròn đến chữ số thập phân thứ hai).

Tìm ĐKXĐ của \(\sqrt A \) khi và chỉ khi \(A \ge 0\)

Thay x = 5 vào biểu thức A để tính

ĐKXĐ: 3x + 6 \( \ge \) 0 suy ra x \( \ge \) - 2

Thay x = 5 vào A = \(\sqrt {3x + 6} \), ta được: A = \(\sqrt {3.5 + 6} = \sqrt {21} \approx 4,58\)

Thực hành8

Trả lời câu hỏi Thực hành 8 trang 40

Cho biểu thức P = \(\sqrt {{a^2} - {b^2}} \). Tính giá trị của P khi:

a) a = 5; b = 0

b) a = 5; b = -5

c) a = 2; b = -4

Thay lần lượt a và b vào biểu thức P để tính.

a) Thay a = 5; b = 0 vào P = \(\sqrt {{a^2} - {b^2}} \), ta được:

P = \(\sqrt {{5^2} - {0^2}} = 5\)

b) Thay a = 5; b = -5 vào P = \(\sqrt {{a^2} - {b^2}} \), ta được:

P = \(\sqrt {{5^2} - {{( - 5)}^2}} = 0\)

c) Thay a = 2; b = -4 vào P = \(\sqrt {{a^2} - {b^2}} \) thì biểu thức P không khác định vì

a² – b² = -12 < 0 .

Vận dụng2

Trả lời câu hỏi Vận dụng 2 trang 40

Một trạm phát sóng được đặt ở vị trí B cách đường tàu một khoảng AB = 300 m. Đầu tàu đang ở vị trí C, cách vị trí A một khoảng AC = x (m) (Hình 4)

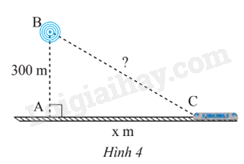
a) Viết biểu thức (theo x) biểu thị khoảng cách từ trạm phát sóng đến đầu tàu.

b) Tính khoảng cách trên khi x = 400; x = 1000 (kết quả làm tròn đến hàng đơn vị của mét).

Sử dụng định lí Pythagore vào tam giac vuông ABC có:

BC² = AB² + AC² .

Thay lần lượt giá trị x để tính khoảng cách

a) Ta có khoảng cách từ trạm phát sóng đến đầu tàu là: \(\sqrt {{{300}^2} + {x^2}} \) (m)

b) Thay x = 400 thì khoảng cách từ trạm phát sóng đến đầu tàu là: \(\sqrt {{{300}^2} + {{400}^2}} = 500\) (m)

Thay x = 1000 thì khoảng cách từ trạm phát sóng đến đầu tàu là: \(\sqrt {{{300}^2} + {{1000}^2}} \approx 1044\) (m)