
Giải tam giác ABC vuông tại A, biết:
a) \(AC = 11cm,\widehat C = {60^o}\);
b) \(BC = 20cm,\widehat C = {35^o}\);
c) \(AB = 7cm,AC = 12cm\);
d) \(AB = 9cm,BC = 20cm\).

Tam giác ABC vuông tại A nên:
a) \(\widehat B = {90^o} - \widehat C\), \(AB = AC.\tan C\), \(BC = \frac{{AC}}{{\cos C}}\)
b) \(\widehat B = {90^o} - \widehat C\), \(AB = BC.\sin C\), \(AC = BC.\cos C\)
c) \(B{C^2} = A{B^2} + A{C^2}\), \(\tan B = \frac{{AC}}{{AB}} = \frac{{12}}{7}\) từ đó tính được góc B, \(\widehat C = {90^o} - \widehat B\).
d) \(A{C^2} = B{C^2} - A{B^2}\), \(\sin C = \frac{{AB}}{{BC}}\) từ đó tính được góc C, \(\widehat B = {90^o} - \widehat C\).

Advertisements (Quảng cáo)
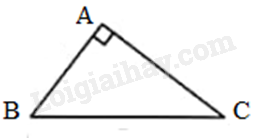
Tam giác ABC vuông tại A nên:
a) \(\widehat B = {90^o} - \widehat C = {90^o} - {60^o} = {30^o}\).
\(AB = AC.\tan C = 11.\tan {60^o} = 11\sqrt 3 \approx 19,1cm\),
\(BC = \frac{{AC}}{{\cos C}} = \frac{{11}}{{\cos {{60}^o}}} = 22\left( {cm} \right)\)
b) \(\widehat B = {90^o} - \widehat C = {90^o} - {35^o} = {55^o}\).
\(AB = BC.\sin C = 20.\sin {35^o} \approx 11,5cm\),
\(AC = BC.\cos C = 20.\cos {35^o} \approx 16,4\left( {cm} \right)\).
c) \(B{C^2} = A{B^2} + A{C^2} = {7^2} + {12^2} = 193\) nên \(BC \approx 13,9cm\).
\(\tan B = \frac{{AC}}{{AB}} = \frac{{12}}{7}\) nên \(\widehat B \approx {59^o}45’\), \(\widehat C = {90^o} - \widehat B \approx {30^o}15’\).
d) \(A{C^2} = B{C^2} - A{B^2} = {20^2} - {9^2} = 319\) nên \(AC \approx 17,9cm\).
\(\sin C = \frac{{AB}}{{BC}} = \frac{9}{{20}}\) nên \(\widehat C \approx {26^o}45’\), \(\widehat B = {90^o} - \widehat C \approx {63^o}15’\).
