Giải mục 3 trang 68, 69 Toán 9 Cùng khám phá tập 1: Tìm công thức tính thể tích V của hình lập phương có cạnh bằng a...

Hoạt động2

Trả lời câu hỏi Hoạt động 2 trang 68

Tìm công thức tính thể tích V của hình lập phương có cạnh bằng a. Từ đó giải thích vì sao $a = \sqrt[3]{V}$.

Sử dụng công thức tính thể tích V của hình lập phương.

Công thức tính thể tích V của hình lập phương có cạnh bằng a là: $V = {a^3}$. Do đó, $a = \sqrt[3]{V}$.

Vận dụng2

Trả lời câu hỏi Vận dụng 2 trang 69

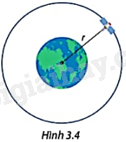
Bán kính r(m) của quỹ đạo của một vệ tinh (giả sử quỹ đạo của vệ tinh là đường tròn) được ước tính bởi công thức $r = \sqrt[3]{{\frac{{GM{t^2}}}{{4{\pi ^2}}}}}$, trong đó $G\left( {N{m^2}/k{g^2}} \right)$ là hằng số hấp dẫn vũ trụ, M(kg) là khối lượng của Trái Đất và t(s) là thời gian để vệ tinh hoàn thành một quỹ đạo (nguồn: http://courses.lumenlearning.com/suny-osuniversityphysics/chapter/13-4-satellite-orbits-and-energy/). Hãy ước tính bán kính của quỹ đạo của vệ tinh có thời gian hoàn thành một quỹ đạo là $2,{6.10^6}$ giây, biết rằng $G = \frac{{6,67}}{{{{10}^{11}}}}\left( {N{m^2}/k{g^2}} \right)$ và $M = 5,{98.10^{24}}\left( {kg} \right)$ (làm tròn kết quả đến hàng nghìn).

Căn bậc ba của một số thực a là số x sao cho ${x^3} = a$.

Thay $G = \frac{{6,67}}{{{{10}^{11}}}},M = 5,{98.10^{24}},t = 2,{6.10^6}$ thay vào công thức $r = \sqrt[3]{{\frac{{GM{t^2}}}{{4{\pi ^2}}}}}$ ta có:

$r = \sqrt[3]{{\frac{{\frac{{6,67}}{{{{10}^{11}}}}.5,{{98.10}^{24}}.{{\left( {2,{{6.10}^6}} \right)}^2}}}{{4{\pi ^2}}}}} \approx 408\;763\;000$.