
Một hãng viễn thông nước ngoài có hai gói cước như sau:
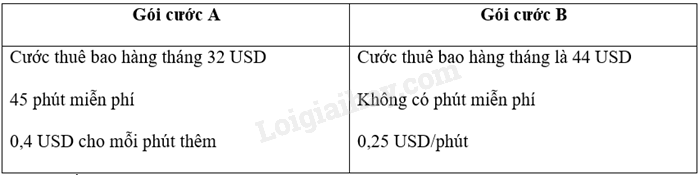
a) Hãy viết một phương trình xác định thời gian gọi (phút) mà phí phải trả trong cùng một tháng của hai gói cước là như nhau và giải phương trình đó.
b) Nếu khách hàng chỉ gọi tối đa là 180 phút trong 1 tháng thì nên dùng gói cước nào? Nếu khách hàng gọi 500 phút trong 1 tháng thì nên dùng gói cước nào?

a) Gọi thời gian gọi là x (phút) \(\left( {x > 0} \right)\)
Biểu diễn số tiền phải trả khi gọi x phút đối với gói cước A, B. (Đối với gói cước A có 2 trường hợp:
\(TH1:x \le 45\)
\(TH2:x > 45\)
Xác định phương trình cần tìm và giải.
b) Ta cần tính số chi phí phải trả khi dùng cả hai gói cước, từ đó ta có lựa chọn gói cước cho phù hợp.

a) Gọi thời gian gọi trong một tháng là x (phút) \(\left( {x > 0} \right)\)
Số tiền phải trả khi gọi x phút đối với gói cước B là \(44 + 0,25.x\) (USD)
Advertisements (Quảng cáo)
Số tiền phải trả khi x phút đối với gói cước A là
\(TH1:x \le 45\) thì phí trả là 32 USD.
\(TH2:x > 45\) thì phí trả là \(32 + 0,4.\left( {x - 45} \right)\)
Vì số tiền phải trả của gói cước B lớn hơn 44 nên để phí trả hai gói cước trong cùng một tháng của hai gói cước là như nhau thì đối với gói cước A thì sẽ rơi vào trường hợp thứ hai nên ta có phương trình:
\(44 + 0,25.x = 32 + \left( {x - 45} \right).0,4\)
\(0,25.x - 0,4x = - 44 + 32 - 45.0,4\)
\( - 0,15x = - 30\)
\(x = 200\left( {t/m} \right).\)
Vậy khi gọi 180 phút thì chi phí phải trả đối với hai gói cước là như nhau.
b) Ta có bất phương trình biểu thị thời gian gọi mà chi phí gói cước A lớn hơn gói cước B là:
\(\begin{array}{l}32 + \left( {x - 45} \right).0,4 > 44 + 0,25x\\32 + 0,4x - 18 > 44 + 0,25x\\0,4x - 0,25x > 44 - 32 + 18\\0,15x > 30\\x > 200\end{array}\)
Suy ra với thời gian gọi lớn hơn 200 phút thì chi phí phải trả theo gói cước A lớn hơn chi phí phải trả theo gói cước B.
Vậy nếu khách hàng chỉ dùng tối đa 180 phút (< 200) trong một tháng thì nên dùng gói cước A;
nếu khách hàng dùng khoảng 500 phút (> 200) trong một tháng thì nên dùng gói cước B.
