
Xét các tam giác vuông có một góc nhọn bằng hai lần góc nhọn còn lại. Hỏi các tam giác đó có đồng dạng với nhau không? Tính sin và cos của góc nhọn lớn hơn.

Ta xét tam giác ABC vuông, với điều kiện có một góc nhọn bằng hai lần góc nhọn còn lại, ta sẽ tính được số đo của góc B và góc C. Từ đó ta thấy rằng cứ tam giác vuông nào có điều kiện như vậy ta đều tính được góc B và góc C. Do đó ta thấy hai tam giác vuông có một góc nhọn bằng hai lần góc nhọn còn lại có đồng dạng với nhau. Khi tính được số đo góc, ta sử dụng MTCT để tính kết quả.

Advertisements (Quảng cáo)
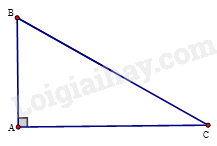
Xét tam giác ABC vuông tại A, có \(\widehat B = 2\widehat C\) mà \(\widehat B + \widehat C = {90^0}\) nên ta có \(2\widehat C + \widehat C = {90^0}\) suy ra \(\widehat C = {30^0}\) do đó \(\widehat B = {60^0}\)
Nên các tam giác vuông có một góc nhọn bằng hai lần góc nhọn còn lại thì sẽ đồng dạng với nhau, do có các góc tương ứng bằng nhau.
\(\sin \widehat B = \sin {60^0} = \frac{{\sqrt 3 }}{2};\cos \widehat B = \cos {60^0} = \frac{1}{2}\)
