
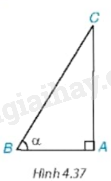
Cho tam giác ABC vuông tại A, có \(\widehat B = \alpha \) (H.4.37).
a) Hãy viết các tỉ số lượng giác \(\sin \alpha ;\cos \alpha \)
b) Sử dụng định lý Pythagore, chứng minh rằng \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)

Tỉ số giữa cạnh đối và cạnh huyền là \(\sin \alpha \)
Advertisements (Quảng cáo)
Tỉ số giữa cạnh kề với cạnh huyền là \(\cos \alpha \)
Định lý Pythagore: cạnh huyền bình phương bằng tổng bình phương của hai cạnh góc vuông.

a) Ta có \(\sin \alpha = \frac{{AC}}{{BC}};\cos \alpha = \frac{{AB}}{{BC}}\)
b) Tam giác ABC vuông tại A nên ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lý Pythagore)
Nên ta có
\({\sin ^2}\alpha + {\cos ^2}\alpha = {\left( {\frac{{AC}}{{BC}}} \right)^2} + {\left( {\frac{{AB}}{{AC}}} \right)^2} = \frac{{A{C^2} + A{B^2}}}{{B{C^2}}} = \frac{{B{C^2}}}{{B{C^2}}} = 1\) (đpcm).
