
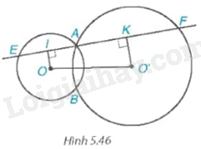
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Một đường thẳng d đi qua A cắt (O) tại E và cắt (O’) tại F (E và F) khác A. Biết điểm A nằm trong đoạn EF. Gọi I và K lần lượt là trung điểm của AE và AF (H.5.46).
a) Chứng minh rằng tứ giác OO’KI là một hình thang vuông.
b) Chứng minh rằng \({\rm{IK}} = \frac{1}{2}{\rm{EF}}\).
c) Khi d ở vị trí nào (d vẫn qua A) thì OO’KI là một hình chữ nhật?

a) Chứng minh OO’KI là hình thang có 1 góc vuông.
b) Áp dụng tính chất trung điểm của đoạn thẳng.
c) Hình thang OO’KI là hình chữ nhật khi và chỉ khi \(\widehat {{\rm{OIO’}}} = 90^\circ \).

a) Tam giác OAE cân tại O có OI là trung tuyến nên OI cũng là đường cao.
Advertisements (Quảng cáo)
Tam giác O’AF cân tại O có O’K là trung tuyến nên O’K cũng là đường cao.
Suy ra: OI // O’K (vì cùng vuông góc với d)
Do đó: OO’KI là hình thang.
Mà: \(\widehat {{\rm{OIA}}} = 90^\circ \)
Vậy OO’KI là một hình thang vuông.
b)
Vì I là trung điểm của AE nên \({\rm{IA}} = \frac{1}{2}{\rm{AE}}\)
Vì K là trung điểm của AF nên \({\rm{AK}} = \frac{1}{2}{\rm{AF}}\)
Suy ra: \({\rm{IK}} = {\rm{IA}} + {\rm{AK}} = \frac{1}{2}{\rm{AE}} + \frac{1}{2}{\rm{AF}} = \frac{1}{2}{\rm{EF}}\)
c) Hình thang OO’KI là hình chữ nhật khi và chỉ khi \(\widehat {{\rm{OIO’}}} = 90^\circ \) hay \({\rm{OI}} \bot {\rm{OO’}}\)
Mà \({\rm{d}} \bot {\rm{OI}}\) nên \({\rm{d//OO’}}\)
