Hoạt động1
Trả lời câu hỏi Hoạt động 1 trang 6
Câu “Quýt, cam mười bảy quả tươi” có nghĩa là tổng số cam và số quýt là 17. Hãy viết hệ thức với hai biến x và y biểu thị giả thiết này.

Phía trên của câu hỏi đã cho: Gọi x là số cam, y là số quýt ( với x, y nguyên dương).
Tổng số cam và số quýt tức là phép tính cộng x quả quýt và y quả cam

Hệ thức biểu thị: \(x + y = 17.\)
Hoạt động2
Trả lời câu hỏi Hoạt động 2 trang 6
Tương tự, hãy viết hệ thức với hai biến x và y biểu thị giả thiết cho bởi các câu thơ thứ ba, thứ tư và thứ năm.
Quýt, cam mười bảy quả tươi
Đem chia cho một trăm người cùng vui.
Chia ba mỗi quả quýt rồi,
Còn cam, mỗi quả chia mười vừa xinh.
Trăm người, trăm miếng ngọt lành.
Quýt, cam mỗi loại tính rành là bao?


- Câu thơ thứ 3 (Chia ba mỗi quả quýt rồi) tức là mỗi quả quýt thì ta sẽ có 3 miếng nên x quả sẽ có \(3x\) miếng
- Câu thơ thứ tư (Còn cam, mỗi quả chia mười vừa xinh) tức là mỗi quả cam thì ta sẽ có 10 miếng nên y quả sẽ có \(10y\) miếng
- Trăm người trăm miếng tức là số miếng quýt (\(3x\) miếng) và số miếng cam (\(10y\) miếng) tổng là 100 miếng

Hệ thức liên hệ giữa x và y qua các câu thơ thứ ba, thứ tư và thứ năm là \(3x + 10y = 100.\)
Luyện tập1
Trả lời câu hỏi Luyện tập 1 trang 6
Hãy viết một phương trình bậc nhất hai ẩn và chỉ ra một nghiệm của nó.

Phương trình bậc nhất hai ẩn x và y là hệ thức dạng \(ax + by = c\left( 1 \right)\) trong đó a,b và c là các số đã biết \(a \ne 0\) hoặc \(b \ne 0.\) Nên ta có thể chọn a, b,c là số thực bất kì.
Nếu thay \(x = {x_0};y = {y_0}\) vào phương trình số \(\left( 1 \right)\) thì ta có \(a{x_0} + b{y_0} = c\) là một khẳng định đúng thì \(\left( {{x_0};{y_0}} \right)\) là nghiệm của phương trình \(\left( 1 \right)\)

Advertisements (Quảng cáo)
Ta có \(2x - y = 5\) là một phương trình bậc nhất hai ẩn.
Cặp số \(\left( {3;1} \right)\) là một nghiệm của phương trình \(2x - y = 5\) vì \(2.3 - 1 = 5.\) (luôn đúng).
Luyện tập2
Trả lời câu hỏi Luyện tập 2 trang 8
Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:
a) \(2x - 3y = 5;\)
b) \(0x + y = 3;\)
c) \(x + 0y = - 2.\)

Để viết nghiệm của một phương trình bậc nhất hai ẩn, ta cần rút y theo x \(\left( {by = c - ax} \right)\) từ đó ta giải được \(y = \frac{{c - ax}}{b}\) với \(b \ne 0.\) Đối với trường hợp \(b = 0\) thì ta làm ngược lại (rút x theo y).
Biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn là đường thẳng \(ax + by = c.\)

a) \(2x - 3y = 5;\)
Ta có \(y = \frac{{2x - 5}}{3}\) nên mỗi cặp số \(\left( x;\frac{{2x - 5}}{3} \right)\) với \(x \in \mathbb{R}\) tùy ý là một nghiệm của phương trình \(2x - 3y = 5.\)
Biểu diễn hình học tất cả các nghiệm của phương trình \(2x - 3y = 5.\)
Cho \(x = 0 \Rightarrow y = \frac{{ - 5}}{3} \Rightarrow A\left( {0;\frac{{ - 5}}{3}} \right)\)
\(y = 0 \Rightarrow x = \frac{5}{2} \Rightarrow B\left( {\frac{5}{2};0} \right)\)
Đường thẳng \(2x - 3y = 5\) đi qua hai điểm A và B
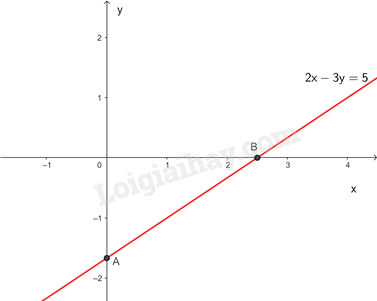
Các nghiệm là tọa độ của một điểm thuộc đường thẳng \(2x - 3y = 5.\)
b) \(0x + y = 3;\)
Ta có \(0x + y = 3\) rút gọn thành \(y = 3\) nên phương trình có nghiệm là \(\left( {x;3} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục hoành và cắt trục tung tại điểm (0;3). Ta gọi đó là đường thẳng y = 3
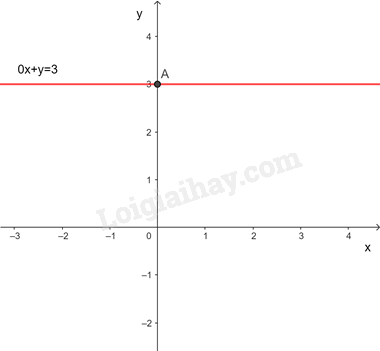
Các nghiệm là tọa độ của một điểm thuộc đường thẳng \(0x + y = 3.\)
c) \(x + 0y = - 2.\)
Ta có \(x + 0y = - 2\) rút gọn thành \(x = - 2\) nên phương trình có nghiệm là \(\left( { - 2;y} \right)\) với \(y \in \mathbb{R}\) tùy ý.
Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục tung và cắt trục hoành tại điểm (-2; 0). Ta gọi đó là đường thẳng x = -2
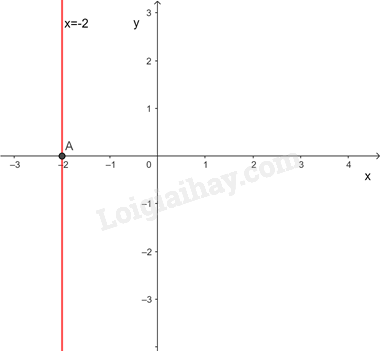
Các nghiệm là tọa độ của một điểm thuộc đường thẳng \(x + 0y = - 2.\)
