a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau:
\(y = {1 \over 2}x + 2\); \(y = -x + 2\)
b) Gọi giao điểm của hai đường thẳng \(y = {1 \over 2}x + 2\) và \(y = -x + 2\) với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C. Tính các góc của tam giác ABC (làm tròn đến độ).
c) Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét)

a) Đồ thị được vẽ như hình dưới:
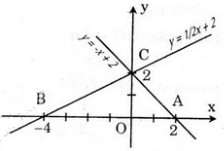
b) Bằng hình vẽ và các phép tính, ta tìm được tọa độ của 3 điểm A, B, C đó là:
\(A(-4;0);B(2;0);C(0;2)\)
Dễ dàng chứng minh được tam giác COB vuông cân tại O (O là gốc tọa độ) nên:
\(\widehat{B}=45^o\)
Advertisements (Quảng cáo)
Dùng công thức lượng giác đối với tam giác AOC vuông tại O, ta có:
\(tanA=\frac{OC}{OA}=\frac{1}{2}\Rightarrow \widehat{A}\approx 26,56^o\)
\(\widehat{C}=180^o-\widehat{A}-\widehat{B}\approx 108,43^o\)
c) Ta có:
\(AB = 6 (cm)\)
\(AC=\sqrt{AO^2+OC^2}=2\sqrt{5}(cm)\)
\(BC=\sqrt{BO^2+OC^2}=2\sqrt{2}(cm)\)
Chu vi tam giác là:
\(P=AB+BC+AC=2(3+\sqrt{5}+\sqrt{2})(cm)\)
Diện tích tam giác:
\(S=\frac{1}{2}CO.AB=\frac{1}{2}.2.6=6(cm^2)\)
