Bài 36. Một chi tiết máy gồm một hình trù và hai nửa hình cầu với các kích thước đã cho trên hình 111 (đơn vị: cm)
a) Tìm một hệ thức giữa \(x\) và \(h\) khi \(AA’\) có độ dài không đổi và bằng \(2a\).
b) Với điều kiện ở a) hãy tính diện tích bề mặt và thể tích của chi tiết theo \(x\) và \(a\).
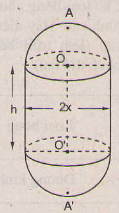

a) Ta có \(h + 2x = 2a\)
b) - Diện tích cần tính gồm diện tích xung quanh của hình trụ có bán kính đáy là \(x\), chiều cao là \(h\) và diện tích mặt cầu có bán kính là \(x\).
- Diện tích xung quanh của hình trụ: \({S_{tru}} = {\rm{ }}2\pi xh\)
- Diện tích mặt cầu:\({S_{cau}} = {\rm{ }}4\pi {x^2}\)
Advertisements (Quảng cáo)
Nên diện tích bề mặt của chi tiết máy là:
\(S{\rm{ }} = {\rm{ }}{S_{tru}} + {S_{cau}}\)
\(= 2\pi xh{\rm{ }} + 4\pi {x^{2}} = 2\pi x\left( {h + 2x} \right){\rm{ }} = {\rm{ }}4\pi ax\)
Thể tích cần tìm gồm thể tích hình trụ và thể tích hình cầu. Ta có:
\({V_{tru}}{\rm{ }} = \pi {x^2}h\)
\({V_{cau}} = {4 \over 3}\pi {x^3}\)
Nên thể tích của chi tiết máy là:
\(V = {V_{tru}} + {V_{cau}} = \pi {x^2}h + {4 \over 3}\pi {x^3}\)
\(= 2\pi {x^2}(a - x) + {4 \over 3}\pi {x^3} = 2\pi {x^2}\left( {a - {1 \over 3}x} \right)\)
