Bài 42. Hãy tính thể tích các hình dưới đây theo kích thước đã cho (h.117).
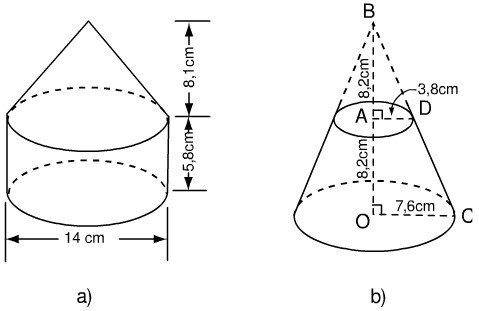

- Hình a:
Thể tích hình trụ có đường kính đáy \(14cm\), đường cao \(5,8cm\)
\({V_1} = {\rm{ }}\pi {\rm{ }}.{\rm{ }}{r^2}h{\rm{ }} = {\rm{ }}\pi .{\rm{ }}{7^2}.{\rm{ }}5,8{\rm{ }} = {\rm{ }}284,2{\rm{ }}\pi {\rm{ }}(c{m^3})\)
Thể tích hình nón có đường kính đáy \(14cm\) và đường cao \(8,1 cm\).
Advertisements (Quảng cáo)
\({V_2} = {1 \over 3}\pi {r^2}h = {1 \over 3}\pi {.7^2}.8,1 = 132,3\pi \left( {c{m^3}} \right)\)
Vậy thể tích hình cần tính là:
\(V{\rm{ }} = {\rm{ }}{V_1} + {\rm{ }}{V_2} = {\rm{ }}2,84,2\pi {\rm{ }} + {\rm{ }}132,3\pi {\rm{ }} = {\rm{ }}416,5\pi {\rm{ }}(c{m^3})\)
- Hình b)
Thể tích hình nón lớn: \({V_1} = {1 \over 3}\pi {r^2}{h_1} = {1 \over 3}\pi {\left( {7,6} \right)^2}.16,4 = 991,47(c{m^3})\)
Thể tích hình nón nhỏ: \({V_2} = {1 \over 3}\pi {r^2}{h_2} = {1 \over 3}\pi {\left( {3,8} \right)^2}.8,2 = 123,93(c{m^3})\)
Thể tích hình nón cần tính là: \(V{\rm{ }} = {\rm{ }}{V_1}-{\rm{ }}{V_2} = {\rm{ }}991,47{\rm{ }}-{\rm{ }}123,93{\rm{ }} = {\rm{ }}867,54{\rm{ }}c{m^3}\)
