Bài 43. Hãy tính thể tích các hình dưới đây theo kích thước đã cho (h.118) (đơn vị : cm).
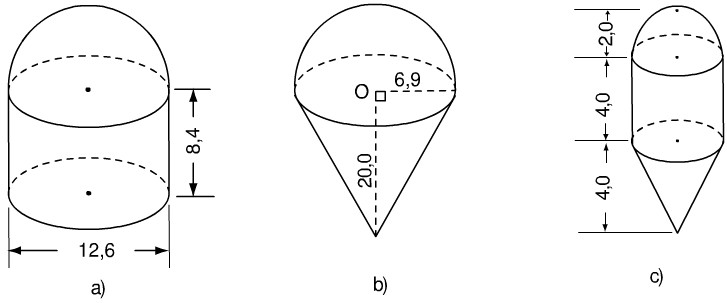

Hình a.
\(\eqalign{
& V = \pi {\left( {{{12,6} \over 2}} \right)^2}.8,4 + {1 \over 2}.{4 \over 3}\pi {\left( {{{12,6} \over 2}} \right)^3} \cr
& = {1 \over 3}\pi {\left( {6,9} \right)^2}.\left( {8,4 + {{12,6} \over 3}} \right) = 500,094\pi \left( {c{m^3}} \right) \cr} \)
Vậy \(V\)hình a = \(500,094π\) cm3
Hình b.
Advertisements (Quảng cáo)
\(\eqalign{
& V = {1 \over 3}\pi {\left( {6,9} \right)^2}.20 + {1 \over 2}.{4 \over 3}\pi .{\left( {6,9} \right)^3} \cr
& = {1 \over 3}\pi {\left( {6,9} \right)^2}\left( {20 + 13,8} \right) = 536,406\pi \left( {c{m^3}} \right) \cr} \)
Vậy \(V\)hình b = \(536, 406π\) cm3
Hình c.
\(V = {1 \over 3}\pi {.2^2}.4 + \pi {.2^2}.4 + {1 \over 2}.{4 \over 3}\pi {.2^3}\)
\(= {4.2^2}.\pi \left( {{1 \over 3} + 1 + {1 \over 3}} \right) = {{80\pi } \over 3}\left( {c{m^3}} \right)\)
Vậy \(V\)hình c = \({{80\pi } \over 3}c{m^3}\)
