Câu hỏi/bài tập:
Bạn An gieo một đồng xu cân đối và bạn Bình rút ngẫu nhiên một tấm thẻ từ hộp chứa 5 tấm thẻ ghi các số 1; 2; 3; 4; 5. Tính xác suất của các biến cố sau:
E: “Rút được tấm thẻ ghi số lẻ”;
F: “Rút được tấm thẻ ghi số chẵn và đồng xu xuất hiện mặt sấp”;
G: “Rút được tấm thẻ ghi số 5 hoặc đồng xu xuất hiện mặt ngửa”.
Cách tính xác suất của một biến cố E:
Bước 1. Mô tả không gian mẫu của phép thử. Từ đó xác định số phần tử của không gian mẫu \(\Omega \).
Bước 2. Chứng tỏ các kết quả có thể của phép thử là đồng khả năng.
Bước 3. Mô tả kết quả thuận lợi của biến cố E. Từ đó xác định số kết quả thuận lợi cho biến cố E.
Bước 4. Lập tỉ số giữa số kết quả thuận lợi cho biến cố E với số phần tử của không gian mẫu \(\Omega \).
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:
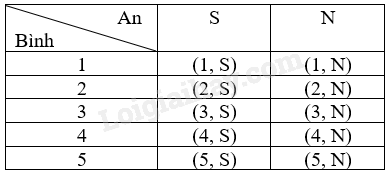
Mỗi ô ở bảng là một kết quả có thể.
Không gian mẫu là
\(\Omega = {(1, S); (2, S); (3, S); (4, S); (5, S); (1, N); (2, N); (3, N); (4, N); (5, N)}.\)
Có 10 kết quả có thể là đồng khả năng.
- Có 6 kết quả thuận lợi cho biến cố E là:
\(\Omega = {(1, S; (3, S); (5, S); (1, N); (3, N); (5, N)}\).
Vậy\(P\left( E \right) = \frac{6}{{10}} = \frac{3}{5}\).
- Có 2 kết quả thuận lợi cho biến cố F là: (2, S); (4, S).
Vậy \(P\left( F \right) = \frac{2}{{10}} = \frac{1}{5}\).
- Có 6 kết quả thuận lợi cho biến cố G là: (5, S); (1, N); (2, N); (3, N); (4, N); (5, N).
Vậy \(P\left( G \right) = \frac{6}{{10}} = \frac{3}{5}\).