Chọn phương án đúng trong mỗi câu sau:
Câu 1
Khi quay hình chữ nhật ABCD quanh cạnh AB ta được một hình trụ có bán kính đáy bằng độ dài đoạn thẳng:
A. AB.
B. CD.
C. AD.
D. AC.

Khi quay hình chữ nhật ABCD một vòng quanh cạnh AB ta được một hình trụ có bán kính đáy bằng độ dài đoạn thẳng AD.

Khi quay hình chữ nhật ABCD một vòng quanh cạnh AB ta được một hình trụ có bán kính đáy bằng độ dài đoạn thẳng AD.
Chọn C
Câu 2
Cho \(\Delta \)ABC vuông tại A có \(AB = 4cm,BC = 5cm\). Khi quay \(\Delta \)ABC quanh cạnh AC ta được một hình nón có chiều cao bằng:
A. 4cm.
B. 3cm.
C. 5cm.
D. 9cm.

+ Khi quay \(\Delta \)ABC quanh cạnh AC ta được một hình nón có chiều cao là AC.
+ Áp dụng định lý Pythagore vào \(\Delta \)ABC vuông tại A, tính được AC.

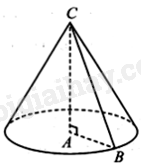
Khi quay \(\Delta \)ABC quanh cạnh AC ta được một hình nón có chiều cao là AC.
Áp dụng định lý Pythagore vào \(\Delta \)ABC vuông tại A ta có: \(A{B^2} + A{C^2} = B{C^2}\)
\({4^2} + A{C^2} = {5^2}\)
\(AC = \sqrt {25 - 16} = 3\left( {cm} \right)\)
Chọn B
Câu 3
Diện tích mặt cầu tâm O, đường kính 10cm là:
A. \(10\pi \;c{m^2}\).
B. \(400\pi \;c{m^2}\).
C. \(50\pi \;c{m^2}\).
Advertisements (Quảng cáo)
D. \(100\pi \;c{m^2}\).

Diện tích mặt cầu có bán kính R là: \(S = 4\pi {R^2}\).

Bán kính của mặt cầu là: \(R = 10:2 = 5\left( {cm} \right)\).
Diện tích mặt cầu là: \(S = 4\pi {.5^2} = 100\pi \left( {c{m^2}} \right)\).
Chọn D
Câu 4
Cho hình nón có bán kính đáy \(r = 2cm\), độ dài đường sinh \(l = 5cm\). Diện tích xung quanh của hình nón đã cho bằng:
A. \(\frac{{10\pi }}{3}\;c{m^2}\).
B. \(\frac{{50\pi }}{3}\;c{m^2}\).
C. \(20\pi \;c{m^2}\).
D. \(10\pi \;c{m^2}\).

Diện tích xung quanh của hình nón bán kính đáy r và độ dài đường sinh l là: \({S_{xq}} = \pi rl\).

Diện tích xung quanh hình nón là: \(S = \pi .2.5 = 10\pi \left( {c{m^2}} \right)\)
Chọn D
Câu 5
Một mặt phẳng đi qua tâm mặt cầu cắt mặt cầu theo một đường tròn có diện tích \(9\pi \;c{m^2}\). Thể tích của mặt cầu bằng:
A. \(972\pi \;c{m^3}\).
B. \(36\pi \;c{m^3}\).
C. \(6\pi \;c{m^3}\).
D. \(81\pi \;c{m^3}\).

+ Tính bán kính R của hình tròn đi qua tâm.
+ Bán kính hình cầu bằng bán kính đường tròn đi qua tâm hình cầu.
+ Thể tích của hình cầu bán kính R là: \(V = \frac{4}{3}\pi {R^3}\).

Vì hình tròn đi qua tâm mặt cầu có diện tích \(9\pi \;c{m^2}\) nên ta có: \(\pi {R^2} = 9\pi \) nên bán kính hình tròn đi qua tâm là \(R = 3\). Vì bán kính hình cầu bằng bán kính đường tròn đi qua tâm mặt cầu nên \(R = 3\).
Thể tích mặt cầu là: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.3^3} = 36\pi \left( {c{m^3}} \right)\)
Chọn B
