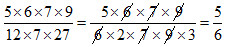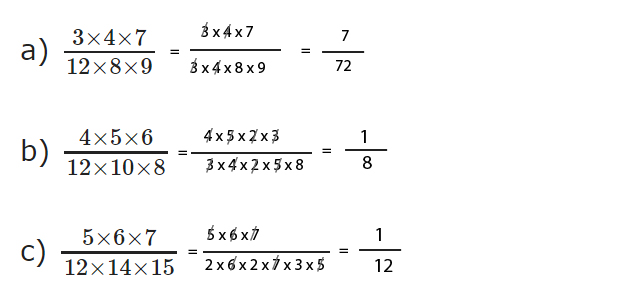1. Quy đồng mẫu số hai phân số:
a) \({5 \over 8}\) và \({8 \over 5}\)
b) \({7 \over 9}\) và \({{19} \over {45}}\)
c) \({8 \over {11}}\) và \({3 \over 4}\)
d) \({{17} \over {72}}\) và \({5 \over {12}}\)
2. Quy đồng mẫu số các phân số (theo mẫu):
Mẫu: Quy đồng mẫu số các phân số \({2 \over 3};{1 \over 4}\) và \({3 \over 5}\)
\({2 \over 3} = {{2 \times 4 \times 5} \over {3 \times 4 \times 5}} = {{40} \over {60}};{1 \over 4} = {{1 \times 3 \times 5} \over {4 \times 3 \times 5}} = {{15} \over {60}};{3 \over 5} = {{3 \times 3 \times 3} \over {5 \times 3 \times 4}} = {{36} \over {40}}\)
Vậy : Quy đồng mẫu số của \({2 \over 3};{1 \over 4}\) và \({3 \over 5}\) được \({{40} \over {60}};{{15} \over {60}};{{36} \over {60}}\)
a) \({1 \over 2};{2 \over 5}\) và \({4 \over 7}\)
b) \({3 \over 2};{2 \over 3}\) và \({5 \over 7}\)
3. Tính theo mẫu:
Mẫu: 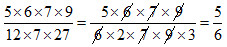
a) \({{3 \times 4 \times 7} \over {12 \times 8 \times 9}}\)
b) \({{4 \times 5 \times 6} \over {12 \times 10 \times 8}}\)
c) \({{5 \times 6 \times 7} \over {12 \times 14 \times 15}}\)

1.
a) Ta có: \({5 \over 8} = {{5 \times 5} \over {8 \times 5}} = {{25} \over {40}};{8 \over 5} = {{8 \times 8} \over {5 \times 8}} = {{64} \over {40}}\)
Advertisements (Quảng cáo)
Vậy quy đồng mẫu số của \({5 \over 8}\) và \({8 \over 5}\) được \({{25} \over {40}}\) và \({{64} \over {40}}.\)
b) Ta có: \({7 \over 9} = {{7 \times 5} \over {9 \times 5}} = {{35} \over {45}}\)
Vậy quy đồng mẫu số của được \({{35} \over {45}}\) và \({{19} \over {45}}\)
c) Ta có:
\(\eqalign{
& {8 \over {11}} = {{8 \times 4} \over {11 \times 4}} = {{32} \over {44}};{3 \over 4} = {{3 \times 11} \over {4 \times 11}} = {{33} \over {44}} \cr
& \cr} \)
Vậy quy đồng mẫu số của \({8 \over {11}}\) và \({3 \over 4}\) được \({{32} \over {44}}\) và \({{33} \over {44}}\)
d) Ta có \({5 \over {12}} = {{5 \times 6} \over {12 \times 6}} = {{30} \over {72}}\)
Vậy quy đồng mẫu số của \({{17} \over {72}}\) và \({5 \over {12}}\) được \({{17} \over {72}}\) và \({{30} \over {72}}\)
2.
a) Ta có: \({1 \over 2} = {{1 \times 5 \times 7} \over {2 \times 5 \times 7}} = {{35} \over {70}};{4 \over 7} = {{4 \times 2 \times 5} \over {7 \times 2 \times 5}} = {{40} \over {70}}\)
\({2 \over 5} = {{2 \times 2 \times 7} \over {5 \times 2 \times 7}} = {{28} \over {70}}\)
Vậy quy đồng mẫu số của \({1 \over 2};{2 \over 5}\) và \({4 \over 7}\) được \({{35} \over {70}};{{28} \over {70}};{{40} \over {70}}\)
b) Ta có:
\(\eqalign{
& {3 \over 2} = {{3 \times 3 \times 7} \over {2 \times 3 \times 7}} = {{63} \over {42}}; \cr
& {5 \over 7} = {{5 \times 2 \times 3} \over {7 \times 2 \times 3}} = {{30} \over {42}}; \cr
& {2 \over 3} = {{2 \times 2 \times 7} \over {3 \times 2 \times 7}} = {{28} \over {42}} \cr} \)
Vậy quy đồng mẫu của \({3 \over 2};{2 \over 3}\) và \({5 \over 7}\) được \({{63} \over {42}};{{28} \over {42}}\) và \({{30} \over {42}}\)
3.