1. Viết số hoặc tỉ số vào chỗ chấm:
a)
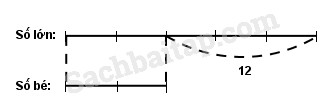
Hiệu của hai số bằng ….
Số lớn được biểu thị là … phần bằng nhau.
Số bé được biểu thị là …. phần như thế.
Tỉ số của số lớn và số bé là ..........
Hiệu số phần bằng nhau là … phần.
b)
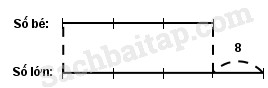
Hiệu của hai số bằng …
Số bé được biểu thị là … phần bằng nhau.
Số lớn được biểu thị là …. phần như thế.
Tỉ số của số bé và số lớn là …
Hiệu số phần bằng nhau là … phần.
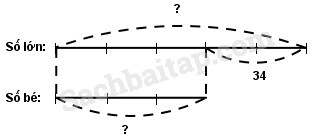
2. Hiệu hai số là 34. Tỉ số của hai số đó là \({5 \over 3}\). Tìm hai số đó.
Ta có sơ đồ:
3. Đoạn đường AB ngắn hơn đoạn đường CD là 2km. Tìm chiều dài mỗi đoạn đường đó, biết ràng chiều dài của đoạn thẳng AB bằng \({3 \over 4}\) chiều dài đoạn thẳng CD.
Bài làm:
1.
a) Tóm tắt:
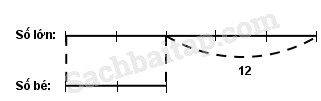
Hiệu của hai số bằng 12.
Số lớn được biểu thị là 5 phần bằng nhau.
Số bé được biểu thị là 2 phần như thế.
Tỉ số của số lớn và số bé là 5 : 2 hay \({5 \over 2}\)
Hiếu số phần bằng nhau là 3 phần.
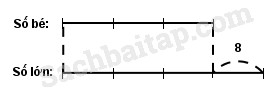
b) Tóm tắt:
Advertisements (Quảng cáo)
Hiệu của hai số bằng 8.
Số bé được biểu thị là 3 phần bằng nhau.
Số lớn được biểu thị là 4 phần như thế.
Tỉ số của số bé và số lớn là 3 : 4 hay \({3 \over 4}\)
Hiệu số phần bằng nhau là 1 phần.
2.
Tóm tắt:
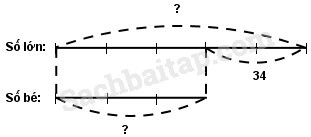

Theo sơ đồ, hiệu số phần bằng nhau:
5 – 3 = 2 (phần)
Số lớn là :
\(34:2 \times 5 = 85\)
Số bé là:
85 – 34 = 51
Đáp số : Số lớn : 85
Số bé : 5
3.
Tóm tắt:
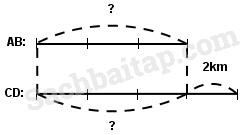

Theo sơ đồ, hiệu số phần bằng nhau:
4 – 3 = 1 (phần)
Đoạn đường AB là:
\(2:1 \times 3 = 6\) (km)
Đoạn đường CD là:
6 + 2 = 8 (km)
Đáp số: Đoạn đường AB 6km
Đoạn đường CD 8km
