
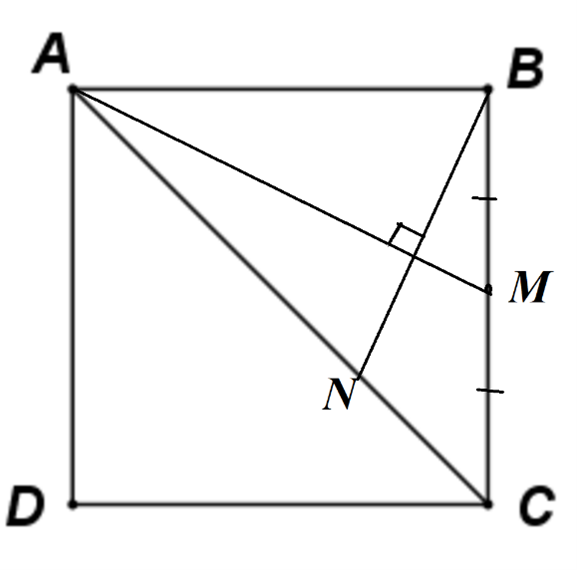
Cho hình vuông ABCD, M là trung điểm của BC. N là điểm nằm giữa hai điểm A và C. Đặt \(x = \frac{{AN}}{{AC}}\). Tìm x thỏa mãn \(AM \bot BN\)

Bước 1: Tách và đưa các vectơ \(\overrightarrow {AM} ,\overrightarrow {BN} \) về vectơ chung gốc sao cho xuất hiện vectơ \(\overrightarrow {AN} ,\overrightarrow {AC} \)
Bước 2: Sử dụng tính chất \(AM \bot BN \Leftrightarrow \overrightarrow {AM} .\overrightarrow {BN} = 0\) để lập PT ẩn x
Bước 3: Giải PT ở bước 2 để tìm x và kết luận

Advertisements (Quảng cáo)
Do \(AM \bot BN\) nên \(\overrightarrow {AM} .\overrightarrow {BN} = 0\)
Ta có: \(x = \frac{{AN}}{{AC}} \Rightarrow AN = xAC \Rightarrow \overrightarrow {AN} = x\overrightarrow {AC} \)
\(\overrightarrow {AM} = \overrightarrow {BM} - \overrightarrow {BA} = \frac{1}{2}\overrightarrow {BC} - \overrightarrow {BA} \) ; \(\overrightarrow {BN} = \overrightarrow {AN} - \overrightarrow {AB} = x\overrightarrow {AC} - \overrightarrow {AB} \)
Khi đó \(\overrightarrow {AM} .\overrightarrow {BN} = 0\)\( \Leftrightarrow \left( {\frac{1}{2}\overrightarrow {BC} - \overrightarrow {BA} } \right).\left( {x\overrightarrow {AC} - \overrightarrow {AB} } \right) = 0\)
\( \Leftrightarrow \frac{x}{2}\overrightarrow {BC} .\overrightarrow {AC} - \frac{1}{2}\overrightarrow {BC} .\overrightarrow {AB} - x\overrightarrow {BA} .\overrightarrow {AC} + \overrightarrow {BA} .\overrightarrow {AB} = 0\)
\( \Leftrightarrow \frac{x}{2}.BC.\sqrt 2 BC.\cos {45^0} + x.AB.\sqrt 2 AB.\cos {45^0} - A{B^2} = 0\)
\( \Leftrightarrow \frac{x}{2} + x - 1 = 0 \Leftrightarrow x = \frac{2}{3}\)
Vậy với \(\frac{{AN}}{{AC}} = \frac{2}{3}\) thì \(AM \bot BN\)
