
Giá bán lúc 10h sáng của một mã cổ phiếu A trong 10 ngày liên tiếp được ghi lại ở biểu đồ sau (đơn vị: nghìn đồng).
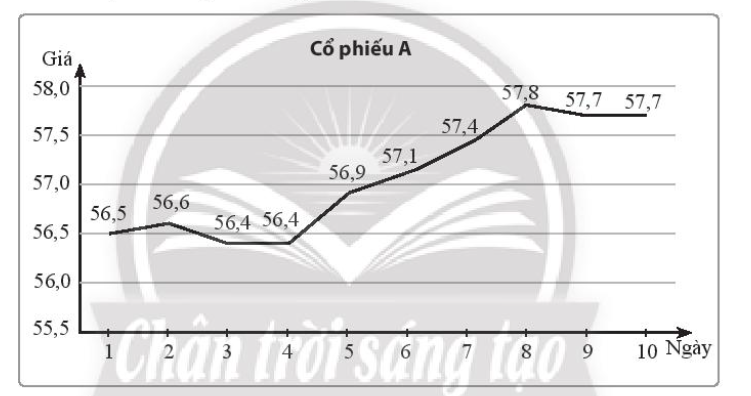
a) Viết mẫu số liệu thống kê giá của mã cổ phiếu A từ biểu đồ trên.
b) Tìm khoảng biến thiện, khoảng tứ phân vị của mẫu số liệu đó.
c) Tính trung bình, độ lệch chuẩn của mẫu số liệu trên.

Bước 1: Sắp xếp số liệu theo thứ tự không giảm: \({x_1},{x_2},...,{x_n}\)
Khoảng biến thiên \(R = {x_n} - {x_1}\)
Bước 2: Tìm trung vị \({Q_2}\) của mẫu số liệu
Bằng \({x_m}\) nếu \(n = 2m - 1\); là \(\frac{1}{2}({x_m} + {x_{m + 1}})\) nếu \(n = 2m\)
Bước 3: Tìm tứ phân vị
Tính \({Q_1}\)là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm trung vị nếu n lẻ)
Tính \({Q_1}\)là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm trung vị nếu n lẻ)
Khoảng tứ phân vị: \(\Delta Q = {Q_3} - {Q_1}\)
Tìm phương sai theo công thức \({S^2} = \frac{1}{n}\left( {{n_1}{x_1}^2 + {n_2}{x_2}^2 + ... + {n_k}{x_k}^2} \right) - {\overline x ^2}\)
Độ lệch chuẩn \(S = \sqrt {{S^2}} \)
Advertisements (Quảng cáo)

a) Bảng thống kê
|
56,4 |
56,4 |
56,5 |
56,6 |
56,9 |
57,1 |
57,4 |
57,7 |
57,7 |
57,8 |
b)
+ Số cao nhất và thấp nhất lần lượt là 57,8 và 56,4 do đó khoảng biến thiên của dãy số liệu trên là: \(R = 57,8 - 56,4 = 1,4\)
+ Tứ phân vị: \({Q_2} = \left( {56,9 + 57,1} \right) = 57\); \({Q_1} = 56,5;{Q_3} = 57,7\)
c)
+ Trung bình của mẫu số liệu là \(\overline x = 57,05\)
+ Phương sai: \({S^2} = 0,2916\)
+ Độ lệch chuẩn: \(S = \sqrt {{S^2}} = 0,54\)
