Giải bài 4.17 trang 54 sách bài tập toán 10 - Kết nối tri thức...

Cho lục giác $ABCDEF.$ Gọi $M,\,\,N,\,\,P,\,\,Q,\,\,R,\,\,S$ theo thứ tự là trung điểm của các cạnh $AB,\;\,BC,\,\,CD,\,\,DE,\,\,EF,\,\,FA.$ Chứng minh rằng hai tam giác $MPR$ và $NQS$ có cùng trọng tâm.

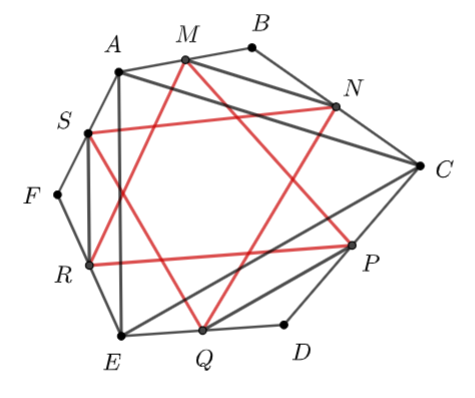
Ta có: $MN$là đường trung bình của $\Delta ABC$

$\Rightarrow$ $\overrightarrow {MN}  = \frac{1}{2}\overrightarrow {AC}$      (1)

Chứng minh tương tự ta được: $\overrightarrow {PQ}  = \frac{1}{2}\overrightarrow {CE}$ và $\overrightarrow {RS}  = \frac{1}{2}\overrightarrow {EA}$     (2)

Từ (1) và (2) $\Rightarrow$ $\overrightarrow {MN}  + \overrightarrow {PQ}  + \overrightarrow {RS}  = \frac{1}{2}\left( {\overrightarrow {AC}  + \overrightarrow {CE}  + \overrightarrow {EA} } \right) = \frac{1}{2}\left( {\overrightarrow {AE}  + \overrightarrow {EA} } \right) = \overrightarrow 0$

$\Rightarrow$ hai tam giác $MPR$ và $NQS$ có cùng trọng tâm.