
Cho tam giác \(ABC\) có trực tâm \(H,\) trọng tâm \(G\) và tâm đường tròn ngoại tiếp \(O.\)
a) Gọi \(M\) là trung điểm của \(BC.\) Chứng minh rằng \(\overrightarrow {AH} = 2\overrightarrow {OM} .\)
b) Chứng minh rằng \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} .\)
c) Chứng minh rằng ba điểm \(G,\,\,H,\,\,O\) cùng thuộc một đường thẳng.

- Chứng minh tứ giác \(ABHC\) là hình bình hành
- Chứng minh \(MO\) là đường trung bình của \(\Delta AA’H\)
- Chứng minh \(\overrightarrow {OB} + \overrightarrow {OC} = 2\overrightarrow {OM} \) từ đó rút ra kết luận \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} .\)
- Chứng minh \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} .\)
- Chứng minh \(\overrightarrow {OH} \) và \(\overrightarrow {OG} \) cùng phương

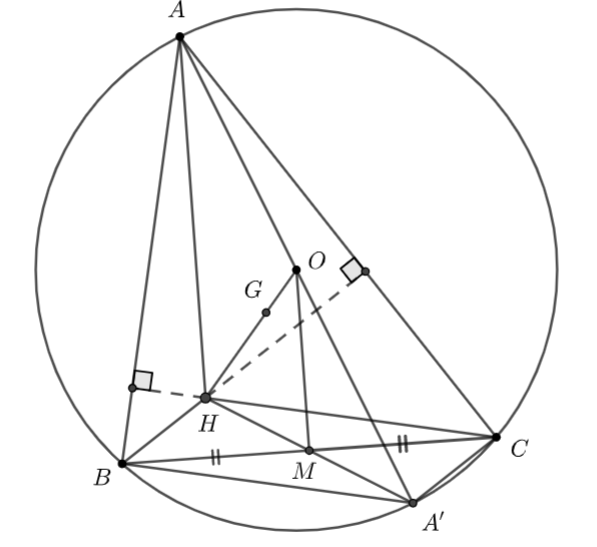
a) Xét \((O)\) có: \(\widehat {ABA’} = \widehat {ACA’} = {90^ \circ }\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow A’C \bot AC\) và \(A’B \bot AB\) (1)
Ta có: \(H\) là trực tâm của tam giác \(ABC.\)
\( \Rightarrow BH \bot AC\) và \(CH \bot AB\) (2)
Từ (1) và (2) \( \Rightarrow \) \(BH\)//\(A’C\) và \(A’B\)//\(CH.\)
Advertisements (Quảng cáo)
Xét tứ giác \(ABHC\) có: \(BH\)//\(A’C\) và \(A’B\)//\(CH\)
\( \Rightarrow \) tứ giác \(ABHC\) là hình bình hành (dấu hiệu nhận biết)
\( \Rightarrow \overrightarrow {BH} = \overrightarrow {A’C} \)
Ta có: tứ giác \(ABHC\) là hình bình hành
nên \(M\) là trung điểm của \(A’H\)
Xét \(\Delta AA’H\) có: \(M\) là trung điểm của \(A’H\)
\(O\) là trung điểm của \(AA’\)
\( \Rightarrow \) \(MO\) là đường trung bình của \(\Delta AA’H\)
\( \Rightarrow \) \(MO\)//\(AH\) và \(2MO = AH\)
\( \Rightarrow \) hai vectơ \(\overrightarrow {MO} ,\,\,\overrightarrow {AH} \) cùng hướng và \(2\overrightarrow {OM} = \overrightarrow {AH} .\)
b) Ta có:
\(\overrightarrow {OB} + \overrightarrow {OC} = \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MC} } \right) = 2\overrightarrow {OM} + \left( {\overrightarrow {MB} + \overrightarrow {MC} } \right) = 2\overrightarrow {OM} \)
Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OA} + 2\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {AH} = \overrightarrow {OH} \) (3)
c) Ta có: \(G\) là trọng tâm của \(\Delta ABC\)
nên \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} .\) (4)
Từ (3) và (4) \( \Rightarrow \overrightarrow {OH} = 3\overrightarrow {OG} \)
\( \Rightarrow \overrightarrow {OH} \) và \(\overrightarrow {OG} \) cùng phương
hay ba điểm \(G,\,\,H,\,\,O\) cùng thuộc một đường thẳng.
