
Với mỗi hàm số dưới đây, hãy vẽ đồ thị, tìm tập xác định , tập giá trị, khoảng đồng biến và khoảng nghịch biến của chúng.
a) \(y = |x - 1| + |x + 1|\)
b) \(y = \left\{ \begin{array}{l}x + 1,x < - 1\\{x^2} - 1,x \ge - 1\end{array} \right.\)

a) Ta có bảng xét dấu sau:
Từ bảng xét dấu suy ra:
- Với x < -1 thì hàm số có dạng \(y = 1 - x - x - 1 \Leftrightarrow y = - 2x\)
- Với -1 ≤ x < 1 thì hàm số có dạng \(y = 1 - x + x + 1 \Leftrightarrow y = 2\)
- Với x ≥ 1 thì hàm số có dạng \(y = x - 1 + x + 1 \Leftrightarrow y = 2x\)
Khi đó: \(y = |x - 1| + |x + 1| = \left\{ \begin{array}{l} - 2x,x < - 1\\2, - 1 \le x < 1\\2x,x \ge 1\end{array} \right.\)
Advertisements (Quảng cáo)
Ta có đồ thị:
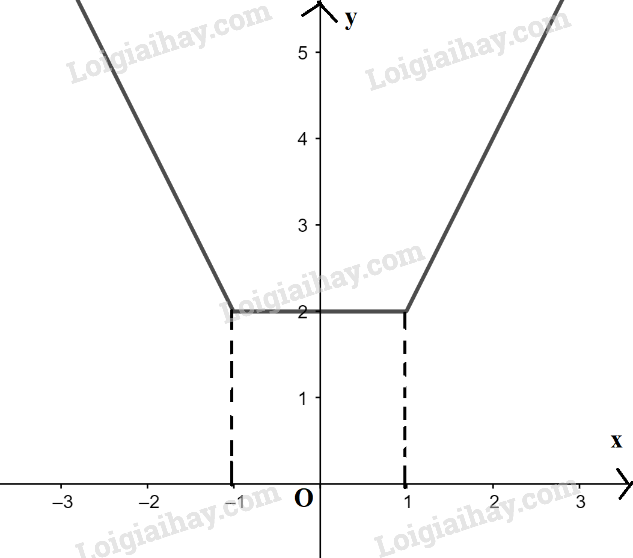
Hàm số \(y = |x - 1| + |x + 1|\) có:
+ Tập xác định là \(\mathbb{R}\)
+ Tập giá trị là \({\rm{[}}2; + \infty )\)
+ Hàm số nghịch biến trên \(( - \infty ; - 1)\), không đổi (hàm hằng) trên (-1 ; 1) và đồng biến trên \((1; + \infty )\)
b) \(y = \left\{ \begin{array}{l}x + 1,x < - 1\\{x^2} - 1,x \ge - 1\end{array} \right.\)
Ta có đồ thị:
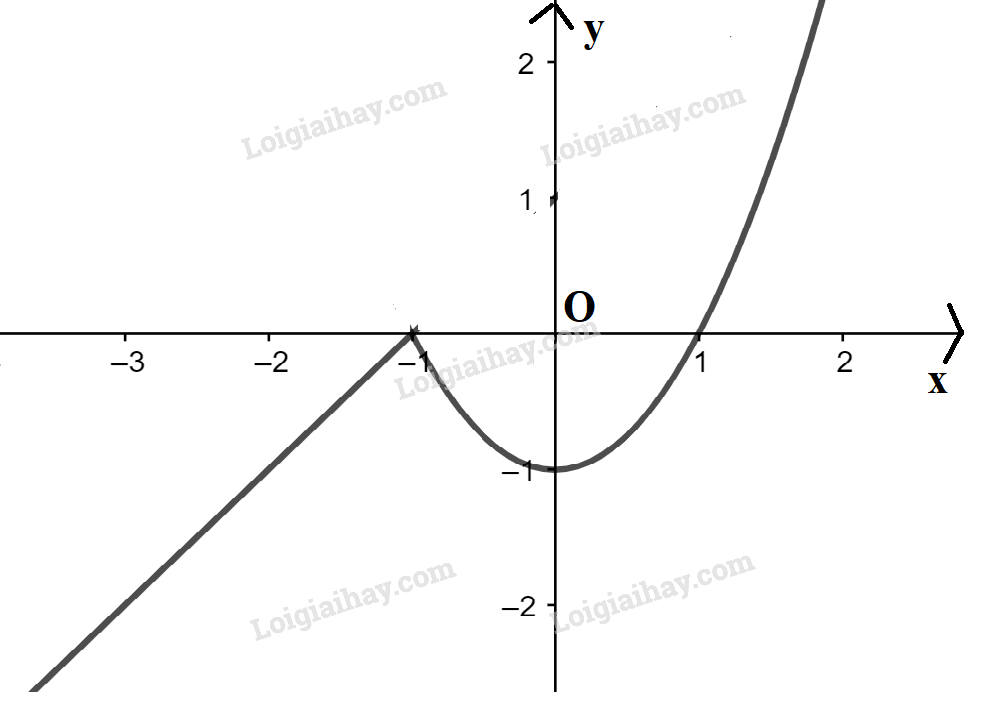
Hàm số \(y = \left\{ \begin{array}{l}x + 1,x < - 1\\{x^2} - 1,x \ge - 1\end{array} \right.\) có:
+ Tập xác định là \(\mathbb{R}\)
+ Tập giá trị là \(\mathbb{R}\)
+ Hàm số đồng biến trên \(( - \infty ; - 1)\) và \((0; + \infty )\); nghịch biến trên (-1 ; 0)
