Hoạt động 2
Cho điểm M trong mặt phẳng toạ độ Oxy.
a) Vē vecto\(\overrightarrow {OM} \).
b) Nêu cách xác định toạ độ của điểm M.

a) Ta có vecto \(\overrightarrow {OM}\) với điểm đầu là O và điểm cuối là M như hình 4.
b) Cách xác định tọa độ điểm M là:
• Từ M kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm H ứng với số a. Số a là hoành độ của điểm M.
• Từ M kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm K ứng với số b. Số b là tung độ của điểm M.
Cặp số (a; b) là toạ độ của điểm M trong mặt phẳng toạ độ Oxy.
Hoạt động 3
Trong mặt phẳng toạ độ Oxy, cho vectơ \(\overrightarrow u \) (Hình 7). Hãy xác định điểm A sao cho \(\overrightarrow {OA} = \overrightarrow u \).

Để xác định điểm A, ta làm như sau (Hình 8):
• Qua O kẻ đường thẳng d song song với giá của vectơ \(\overrightarrow u \).
• Lấy điểm A trên đường thẳng d sao cho hai vectơ \(\overrightarrow {OA} \), \(\overrightarrow u \) cùng hướng và độ dài đoạn thẳng OA bằng độ dài vectơ \(\overrightarrow u \).
Luyện tập – vận dụng 1
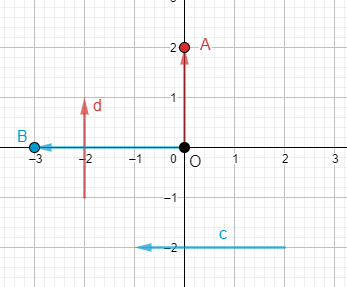
Tìm tọa độ của các vecto \(\overrightarrow c ,\overrightarrow d \) trong Hình 11
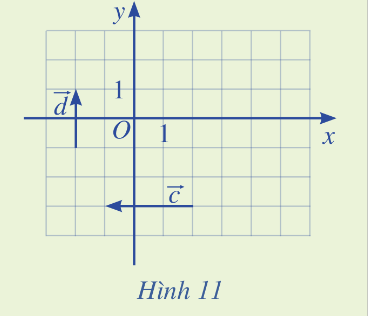

Advertisements (Quảng cáo)
Ta vẽ vecto \(\overrightarrow {OA} = \overrightarrow d \) và \(A\left( {0;2} \right)\). Tọa độ \(\overrightarrow {OA} \) chính là tọa độ của điểm A nên \(\overrightarrow d = \left( {2;2} \right)\)
Ta vẽ vecto \(\overrightarrow {OB} = \overrightarrow c \) và \(A\left( { - 3;0} \right)\). Tọa độ \(\overrightarrow {OB} \) chính là tọa độ của điểm B nên \(\overrightarrow c = \left( { - 3;0} \right)\)
Hoạt động 4
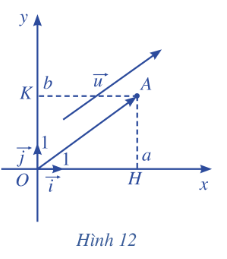
Trong mặt phẳng toạ độ Oxy, cho vectơ\(\overrightarrow u {\rm{ }} = {\rm{ }}\left( {a;{\rm{ }}b} \right)\) . Ta chọn điểm A sao cho\(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) . Xét vectơ đơn vị \(\overrightarrow i \) trên trục hoành Ox và vectơ đơn vị \(\overrightarrow j \) ở trên trục tung Oy (Hình 12).
a) Tìm hoành độ và tung độ của điểm A.
b) Biểu diễn vectơ OH qua vectơ \(\overrightarrow i \).
c) Biểu diễn vectơ OK qua vecto \(\overrightarrow j \).
d) Chứng tỏ rằng\(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \)

a) Do \(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) nên tọa độ vecto \(\overrightarrow {OA} = \left( {a;b} \right)\). Vậy tọa độ điểm A là: \(A\left( {a;b} \right)\)
b) TỌa độ điểm H là \(H\left( {a;0} \right)\) nên \(\overrightarrow {OH} = \left( {a;0} \right)\). Do đó, \(\overrightarrow {OH} = a\overrightarrow i \)
c) TỌa độ điểm K là \(K\left( {0;b} \right)\) nên \(\overrightarrow {OK} = \left( {0;b} \right)\). Do đó, \(\overrightarrow {OK} = b\overrightarrow j \)
d) Ta có: \({\rm{ }}\overrightarrow u = \overrightarrow {OA} {\rm{ }} = \overrightarrow {OH} + \overrightarrow {OK} = a\overrightarrow i + b\overrightarrow j \)( ĐPCM )
Luyện tập – vận dụng 2
Trong mặt phẳng tọa độ Oxy, cho điểm B(-1;0) và vecto \(\overrightarrow v = \left( {0; - 7} \right)\)
a) Biểu diễn vecto \(\overrightarrow v \) qua hai vecto \(\overrightarrow i ,\overrightarrow j \)
b) Biểu diễn vecto \(\overrightarrow {OB} \) qua hai vecto\(\overrightarrow i ,\overrightarrow j \)

a) Vì \(\overrightarrow v = \left( {0; - 7} \right)\)nên \(\overrightarrow v = 0\overrightarrow i + \left( { - 7} \right)\overrightarrow j = - 7\overrightarrow j \)
b) Vì B có tọa độ là (-1; 0) nên \(\overrightarrow {OB} = \left( { - 1;{\rm{ }}0} \right)\). Do đó: \(\overrightarrow {OB} = \left( { - 1} \right)\overrightarrow i + 0\overrightarrow j = - \overrightarrow i \)
