
Cho hình bình hành ABCD
a) Chứng minh \(2\left( {A{B^2} + B{C^2}} \right) = A{C^2} + B{D^2}\)
b) Cho \(AB = 4,BC = 5,BD = 7.\) Tính AC.

a)
Bước 1. Tính góc AC, BD theo AB, BC, cosA dựa vào định lí cosin
Bước 2: Biến đối để suy ra đẳng thức
b) Theo câu a: \(A{C^2} = 2\left( {A{B^2} + B{C^2}} \right) - B{D^2}\), từ đó suy ra AC.
Advertisements (Quảng cáo)

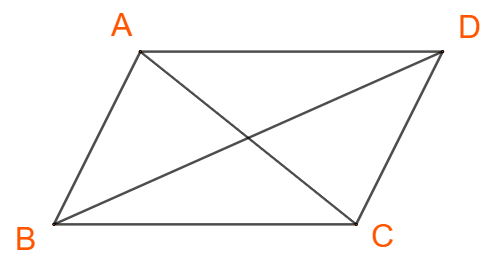
a) Áp dụng định lí cosin ta có:
\(\left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos ABC\\B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos BAD\end{array} \right.\)
Mà \(AD = BC;\cos BAD = \cos ({180^ \circ } - ABC) = - \cos ABC\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}A{C^2} = A{B^2} + B{C^2} + 2.AB.BC.\cos BAD\\B{D^2} = A{B^2} + B{C^2} - 2.AB.AD.\cos BAD\end{array} \right.\end{array}\)
Cộng vế với vế ta được:
\( A{C^2} + B{D^2} = 2\left( {A{B^2} + B{C^2}} \right)\)
b) Theo câu a, ta suy ra: \(A{C^2} = 2\left( {A{B^2} + B{C^2}} \right) - B{D^2}\)
\(\begin{array}{l} \Rightarrow A{C^2} = 2\left( {{4^2} + {5^2}} \right) - {7^2} = 33\\ \Rightarrow AC = \sqrt {33} \end{array}\)
