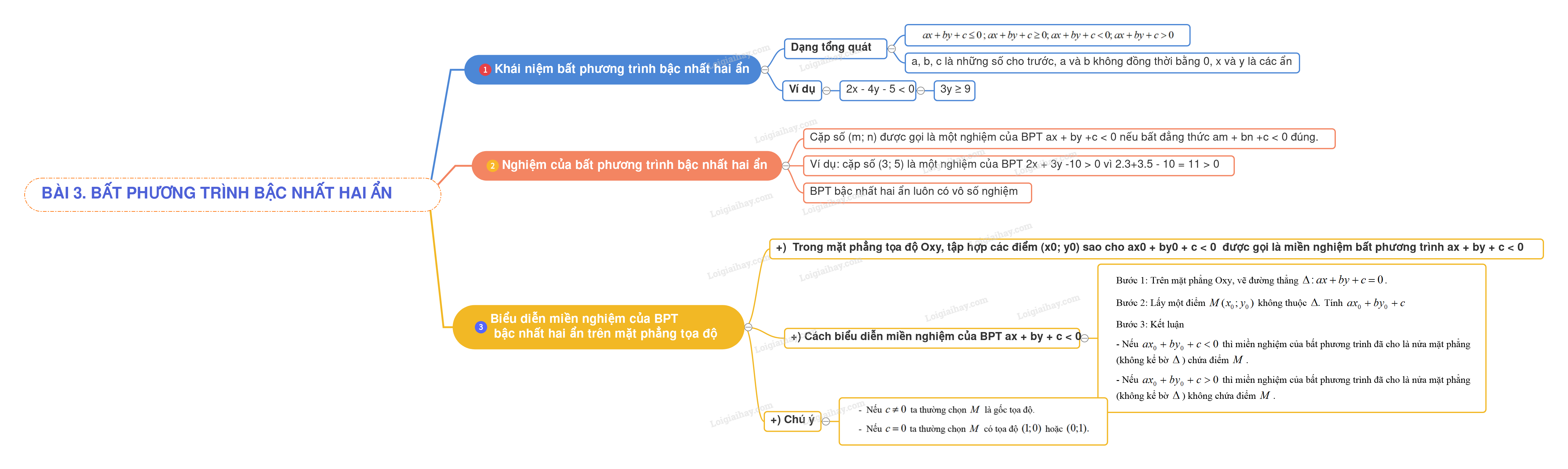
1. Khái niệm bất phương trình bậc nhất hai ẩn
+) Bất phương trình bậc nhất hai ẩn x, y là BPT có một trong các dạng
\(ax + by + c \le 0\;;ax + by + c \ge 0;ax + by + c < 0;ax + by + c > 0\) trong đó a, b, c là những số cho trước, a và b không đồng thời bằng 0, x và y là các ẩn.
Ví dụ: \(2x + 3y - 10 > 0\)
2. Nghiệm của bất phương trình bậc nhất hai ẩn
+) Mỗi cặp số \(({x_0};{y_0})\) thỏa mãn \(a{x_0} + b{y_0} + c\; < 0\) được gọi là một nghiệm của BPT đã cho.
Ví dụ: cặp số \((3;5)\) là một nghiệm của BPT \(2x + 3y - 10 > 0\) vì \(2.3 + 3.5 - 10 = 11 > 0\)
+) BPT bậc nhất hai ẩn luôn có vô số nghiệm.
3. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn
Advertisements (Quảng cáo)
+) Trong mặt phẳng tọa độ Oxy, tập hợp các điểm \(({x_0};{y_0})\) sao cho \(a{x_0} + b{y_0} + c < 0\) được gọi là miền nghiệm của bất phương trình \(ax + by + c < 0\).
+) Biểu diễn miền nghiệm của BPT \(ax + by + c < 0\)
Bước 1: Trên mặt phẳng Oxy, vẽ đường thẳng \(\Delta :ax + by + c = 0\).
Bước 2: Lấy một điểm \(M({x_0};{y_0})\) không thuộc \(\Delta .\) Tính \(a{x_0} + b{y_0} + c\)
Bước 3: Kết luận
- Nếu \(a{x_0} + b{y_0} + c < 0\) thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ \(\Delta \)) chứa điểm \(M\).
- Nếu \(a{x_0} + b{y_0} + c > 0\) thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng (không kể bờ \(\Delta \)) không chứa điểm \(M\).
* Chú ý:
- Nếu \(c \ne 0\) ta thường chọn \(M\) là gốc tọa độ.
- Nếu \(c = 0\) ta thường chọn \(M\) có tọa độ \((1;0)\) hoặc \((0;1).\)