HĐ Khởi động


Áp dụng định lí cosin: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)

Kí hiệu 3 điểm A, B, C như hình dưới.
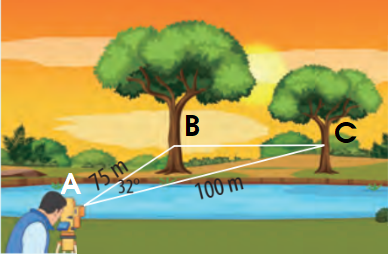
Áp dụng định lí cosin trong tam giác ABC, ta có:
\({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Mà \(b = AC = 100,c = AB = 75,\widehat A = {32^o}\)
\(\begin{array}{l} \Rightarrow {a^2} = {100^2} + {75^2} - 2.100.75.\cos {32^o} \approx 2904,28\\ \Leftrightarrow BC = a \approx 54\end{array}\)
Vậy khoảng cách giữa hai cây bên bờ sông là 54m.
Thực hành
Giải tam giác ABC trong các trường hợp sau:
Advertisements (Quảng cáo)
a) \(a = 17,4;\widehat B = {44^o}30′;\widehat C = {64^o}.\)
b) \(a = 10;b = 6;c = 8.\)

a) Áp dụng định lí sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
b) Áp dụng hệ quả của định lí cosin: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\)

a) Ta cần tính góc \(\widehat A\) và hai cạnh \(b,c.\)
Ta có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {44^o}30′ - {64^o} = {71^o}30′.\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{17,4}}{{\sin {{71}^o}30′}} = \frac{b}{{\sin {{44}^o}30′}} = \frac{c}{{\sin {{64}^o}}}\\ \Rightarrow \left\{ \begin{array}{l}b = \sin {44^o}30′.\frac{{17,4}}{{\sin {{71}^o}30′}} \approx 12,86\\c = \sin {64^o}.\frac{{17,4}}{{\sin {{71}^o}30′}} \approx 16,5\end{array} \right.\end{array}\)
b) Ta cần tính số đo ba góc \(\widehat A,\widehat B,\widehat C\)
Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \cos A = \frac{{{6^2} + {8^2} - {{10}^2}}}{{2.6.8}} = 0;\cos B = \frac{{{{10}^2} + {8^2} - {6^2}}}{{2.10.8}} = \frac{4}{5}\\ \Rightarrow \widehat A = {90^o},\widehat B = {36^o}52’11,63”\\ \Rightarrow \widehat C = {53^o}7’48,37”\end{array}\)
