Hướng dẫn giải bài 3.16 trang 44 SGK Toán lớp 10 tập 1 Kết nối tri thức. Bài tập cuối chương 3 hệ thức lượng trong tam giác
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
a) cos ∠AMB + cos ∠AMC = 0
b) MA2 + MB2 – AB2 = 2MA.MB.cos ∠AMB và MA2 + MC2 – AC2 = 2MA.MC.cos ∠AMC ;
c)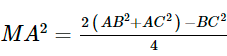 
(công thức đường trung tuyến).
a)
Cos ∠AMB + cos ∠AMC = 0
Ta có: ∠AMB + ∠AMC = 180o
Góc ∠AMC = 180o – ∠AMB
Advertisements (Quảng cáo)
Cos ∠AMB = -cos(180o – ∠AMB) = -cos ∠AMC
=> cos ∠AMB + cos ∠AMC = -cos ∠AMC + cos ∠AMC = 0
b) Xét ΔAMB, ta có:
AB2 = MA2 + MB2 – 2MA.MB.cos ∠AMB
⇔ MA2 + MB2 – AB2 = 2MA.MB.cos ∠AMB (1)
Xét ΔAMC, ta có:
AC2 = MA2 + MC2 – 2MA.MC.cos ∠AMC
⇔ MA2 + MC2 – AC2 = 2MA.MC.cos ∠AMC (2)
c) Cộng vế với vế của (1) với (2), ta được:
MA2 + MB2 – AB2 + MA2 + MC2 – AC2 = 2MA.MB.cos ∠AMB + 2MA.MC.cos ∠AMC
