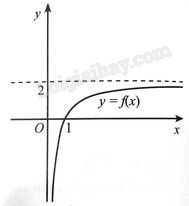
Quan sát đồ thị hàm số trong hình dưới đây và cho biết:
LG a
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\) bằng:
A. \(2\)
B. \(1\)
C. \( + \infty \)
D. \( - \infty \)

Sử dụng đồ thị hàm số để xác định các giới hạn, và tính liên tục của hàm số đó.

Từ đồ thị, ta nhận xét rằng khi \(x \to + \infty \) thì \(f\left( x \right)\) tiến dần tới 2. Do vậy \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\). Đáp án đúng là A.
LG b
\(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right)\) bằng:
A. \(2\)
B. \(1\)
C. \( + \infty \)
Advertisements (Quảng cáo)
D. \( - \infty \)

Sử dụng đồ thị hàm số để xác định các giới hạn, và tính liên tục của hàm số đó.

Từ đồ thị, ta nhận xét rằng khi \(x\) tiến tới 0 về bên phải thì \(f\left( x \right)\) tiến dần tới âm vô cực. Do vậy \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = - \infty \). Đáp án đúng là D.
LG c
Hàm số \(y = f\left( x \right)\) liên tục trên khoảng:
A. \(\left( { - \infty ;1} \right)\)
B. \(\left( { - \infty ; + \infty } \right)\)
C. \(\left( {1; + \infty } \right)\)
D. \(\left( { - \infty ;2} \right)\)

Sử dụng đồ thị hàm số để xác định các giới hạn, và tính liên tục của hàm số đó.

Nhận xét rằng hàm số chỉ nằm ở bên phải trục tung, nên tập xác định của chúng là \(\left( {0, + \infty } \right)\). Suy ra các đáp án A, B, D sai.
Nhận xét rằng trên khoảng \(\left( {1, + \infty } \right)\), đồ thị hàm số là “đường liền”, nên hàm số liên tục trên khoảng \(\left( {1, + \infty } \right)\).
Đáp án đúng là C.
