
Cho khối chóp S.ABC có \(SA \bot \left( {ABC} \right)\), tam giác ABC có độ dài 3 cạnh là \(AB = 5a,BC = 8a,AC = 7a\), góc giữa SB và (ABC) là \({45^0}\). Tính thể tích khối chóp S.ABC.

- Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính:
+ Nếu đường thẳng a vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a với (P) bằng \({90^0}\).
+ Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a và hình chiếu a’ của a trên (P) gọi là góc giữa đường thẳng a và (P).
- Sử dụng kiến thức về thể tích hình chóp: Thể tích hình chóp bằng một phần ba diện tích đáy nhân với chiều cao: \(V = \frac{1}{3}S.h\)

Advertisements (Quảng cáo)
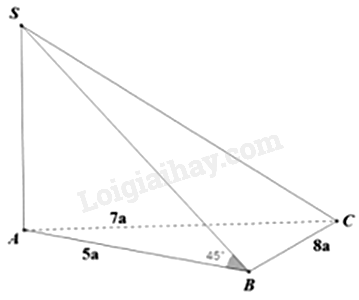
Vì \(SA \bot \left( {ABC} \right)\) nên A là hình chiếu của S trên mặt phẳng (ABC)
Ta có: \(\left( {SB,\left( {ABC} \right)} \right) = \left( {SB,AB} \right) = \widehat {SBA} = {45^0}\)
Vì \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AB\). Do đó, tam giác SAB vuông cân tại A.
Suy ra, \(SA = AB = 5a\).
Nửa chu vi tam giác ABC là: \(p = \frac{{5a + 7a + 8a}}{2} = 10a\)
Diện tích tam giác ABC là: \({S_{ABC}} = \sqrt {10a\left( {10a - 5a} \right)\left( {10a - 7a} \right)\left( {10a - 8a} \right)} = 10{a^2}\sqrt 3 \)
Thể tích khối chóp S. ABC là: \(V = \frac{1}{3}SA.{S_{ABC}} = \frac{1}{3}.5a.10{a^2}\sqrt 3 = \frac{{50{a^3}\sqrt 3 }}{3}\)
