
Một thùng đựng rác có dạng hình chóp cụt tứ giác đều. Đáy và miệng thùng có độ dài lần lượt là 60cm và 120cm, cạnh bên của thùng dài 100cm. Tính thể tích của thùng.

Sử dụng kiến thức về thể tích khối chóp cụt đều: Hình chóp cụt đều có chiều cao h và diện tích hai đáy S, S’ là: \(V = \frac{1}{3}h\left( {S + \sqrt {SS’} + S’} \right)\)

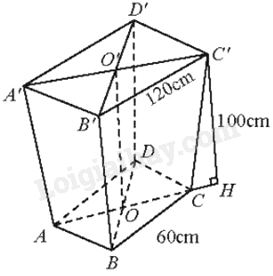
Đặt tên các điểm như hình vẽ.
Advertisements (Quảng cáo)
Kẻ \(C’H \bot AC\left( {H \in AC} \right)\)
Ta có: \(O’C’ \) \( = \frac{{\sqrt {{{120}^2} + {{120}^2}} }}{2} \) \( = 60\sqrt 2 \left( {cm} \right)\), \(OC \) \( = \frac{{\sqrt {{{60}^2} + {{60}^2}} }}{2} \) \( = 30\sqrt 2 \left( {cm} \right)\)
\( \Rightarrow CH \) \( = O’C’ - OC \) \( = 30\sqrt 2 \)
Áp dụng công thức \(V \) \( = \frac{h}{3}\left( {S + \sqrt {S’S} + S’} \right)\)
Với \(h \) \( = C’H \) \( = \sqrt {CC{‘^2} - C{H^2}} \) \( = \sqrt {{{100}^2} - {{\left( {30\sqrt 2 } \right)}^2}} \) \( = 10\sqrt {82} \left( {cm} \right)\), \(S \) \( = {120^2}\left( {c{m^2}} \right),S’ \) \( = {60^2}\left( {c{m^2}} \right)\)
Vậy thể tích thùng là: \(V \) \( = \frac{{10\sqrt {82} }}{3}\left( {{{120}^2} + \sqrt {{{120}^2}{{.60}^2}} + {{60}^2}} \right) \) \( = 84000\sqrt {82} \left( {c{m^3}} \right)\)
