
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh 2a. Mặt phẳng (B’AC) tạo với đáy một góc \({30^0}\), khoảng cách từ B đến mặt phẳng (D’AC) bằng \(\frac{a}{2}\). Tính thể tích khối tứ diện ACB’D’.

+ Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng.
+ Sử dụng kiến thức về thể tích khối tứ diện.

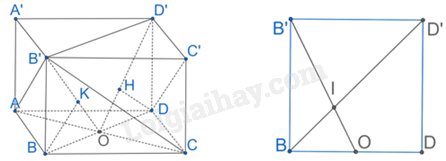
Gọi O là giao điểm của AC và BD.
Ta có: \(AC \bot BD,AC \bot BB’ \) \( \Rightarrow AC \bot \left( {BB’D} \right) \) \( \Rightarrow AC \bot B’O\)
Khi đó, \(BO \bot AC,B’O \bot AC,BO \subset \left( {ABCD} \right),B’O \subset \left( {B’AC} \right)\), AC là giao tuyến của (B’AC) và (ABCD). Do đó, \(\left( {\left( {B’AC} \right),\left( {ABCD} \right)} \right) = \left( {BO,B’O} \right) = \widehat {B’OB} = {30^0}\)
Advertisements (Quảng cáo)
Ta có: \(d\left( {B,\left( {D’AC} \right)} \right) = d\left( {D,\left( {D’AC} \right)} \right) = \frac{a}{2}\)
Chứng minh được: \(AC \bot \left( {BB’D’D} \right) \) \( \Rightarrow \left( {D’AC} \right) \bot \left( {BB’D’D} \right)\) và D’O là giao tuyến của (D’AC) và (BB’D’D).
Từ D kẻ \(DH \bot D’O\left( {H \in D’O} \right)\). Do đó, \(d\left( {D,\left( {D’AC} \right)} \right) = DH = \frac{a}{2}\)
Xét tam giác B’OB vuông tại B có: \(\frac{{BB’}}{{BO}} = \tan {30^0} \) \( \Rightarrow OD = BO = \sqrt 3 BB’\)
Xét tam giác D’DO vuông tại D, đường cao DH có:
\(\frac{1}{{D{H^2}}} = \frac{1}{{O{D^2}}} + \frac{1}{{D'{D^2}}} \) \( \Rightarrow \frac{4}{{{a^2}}} = \frac{1}{{3BB{‘^2}}} + \frac{1}{{D'{D^2}}} \) \( \Rightarrow D’D = \frac{{a\sqrt 3 }}{3} \) \( \Rightarrow OB = a\)
Gọi I là giao điểm của BD’ và B’O, suy ra: \(\frac{{BI}}{{D’I}} = \frac{1}{2} \) \( \Rightarrow d\left( {D’,\left( {B’AC} \right)} \right) = 2d\left( {B,\left( {B’AC} \right)} \right) \) \( \Rightarrow {V_{ACB’D’}} = 2{V_{B’ABC}}\)
Tam giác AOB vuông tại O có: \(OA = \sqrt {A{B^2} - O{B^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \)
Diện tích tam giác ABC là: \({S_{ABC}} = 2{S_{ABO}} = 2.\frac{1}{2}.OB.OA = {a^2}\sqrt 3 \)
Suy ra: \({V_{B’ABC}} = \frac{1}{3}BB’.{S_{ABC}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{3}.{a^2}\sqrt 3 = \frac{{{a^3}}}{3}\). Vậy \({V_{ACB’D’}} = \frac{{2{a^3}}}{3}\)
