
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B. Biết \(AB = a,BC = a\sqrt 3 \), góc giữa hai mặt phẳng (C’AB) và (ABC) bằng \({60^0}\). Tính \({V_{ABC.A’B’C’}}\)

+ Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng.
+ Sử dụng kiến thức về thể tích khối lăng trụ: Thể tích khối lăng trụ bằng diện tích đáy nhân với chiều cao: \(V = S.h\)

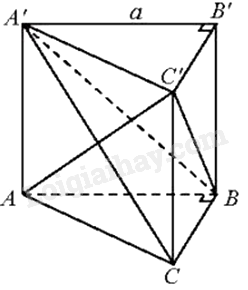
Vì \(AB \bot BC,AB \bot CC’ \Rightarrow AB \bot \left( {BCC’} \right) \Rightarrow AB \bot C’B\)
Advertisements (Quảng cáo)
Ta có: \(AB \bot CB,C’B \bot AB\) và AB là giao tuyến của hai mặt phẳng (C’AB) và (ABC)
Do đó, \(\left( {\left( {C’AB} \right),\left( {ABC} \right)} \right) = \left( {CB,C’B} \right) = \widehat {C’BC} = {60^0}\)
Vì \(CC’ \bot \left( {ABC} \right) \Rightarrow CC’ \bot CB\). Do đó, tam giác C’BC vuông tại C.
Suy ra: \(CC’ = BC.\tan \widehat {C’BC} = a\sqrt 3 .\tan {60^0} = 3a\)
Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}AB.BC = \frac{1}{2}.a.a\sqrt 3 = \frac{{{a^2}\sqrt 3 }}{2}\)
Thể tích hình lăng trụ ABC.A’B’C’ là:
\({V_{ABC.A’B’C’}} = CC’.{S_{ABC}} = 3a.\frac{{{a^2}\sqrt 3 }}{2} = \frac{{3{a^3}\sqrt 3 }}{2}\)
