Bài 39 trang 72 SBT Toán 11 - Kết nối tri thức: Cho hình chóp $S. ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng $a$, đường thẳng $SA$...

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh bằng $a$, đường thẳng $SA$. vuông góc vói mặt phẳng $\left( {ABCD} \right)$ và $SA = a\sqrt 2$.

a) Chứng minh rằng $\left( {SBC} \right) \bot \left( {SAB} \right)$.

b) Tính góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$.

Tính theo $a$ khoảng cách từ điểm $A$ đến mặt phẳng $\left( {SBC} \right)$.

a) Chứng minh $BC \bot \left( {SAB} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)$.

b) Tìm hình chiếu vuông góc của $SC$ trên mặt phẳng $\left( {ABCD} \right)$ là $AC$,

Suy ra góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$ là góc giữa hai đường thẳng $SC$ và $AC$.

Chứng minh tam giác $SAC$ vuông cân tại $A$, suy ra $\widehat {SCA}$

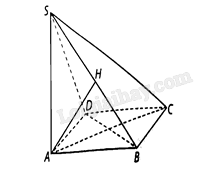
c) Kẻ $AH$ vuông góc với $SB$ tại $H$, chứng minh $AH \bot \left( {SBC} \right)$.

Suy ra khoảng cách từ điểm $A$ đến mặt phẳng $\left( {SBC} \right)$ bằng $AH$.

Xét tam giác $SAB$ vuông tại $A$, tính đường cao $AH$

a) Vì $SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BC$ mà $BC \bot AB \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)$.

b) Vì $SA \bot \left( {ABCD} \right)$ nên đường thẳng $AC$ là hình chiếu vuông góc của $SC$ trên mặt phẳng $\left( {ABCD} \right)$, do đó góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$ là góc giứa hai đường thẳng $SC$ và $AC$.

Ta có: $SA \bot AC$ và $SA = AC = a\sqrt 2$ nên tam giác $SAC$ vuông cân tại $A$, suy ra góc giữa hai đường thẳng $SC$ và $AC$ bằng ${45^ \circ }$.

Vậy góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$ bằng ${45^ \circ }$.

c) Kẻ $AH$ vuông góc với $SB$ tại $H$, vì $BC \bot \left( {SAB} \right)$ nên $BC \bot AH$, suy ra $AH \bot \left( {SBC} \right)$.

Do đó khoảng cách từ điểm $A$ đến mặt phẳng $\left( {SBC} \right)$ bằng $AH$.

Xét tam giác $SAB$ vuông tại $A$, có đường cao $AH$, khi đó:

$AH = \frac{{SA \cdot AB}}{{SB}} = \frac{{a \cdot a\sqrt 2 }}{{\sqrt {{a^2} + 2{a^2}} }} = \frac{{a\sqrt 6 }}{3}.$