
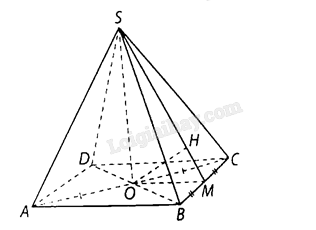
Cho hình chóp đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng a và \(SA = a\sqrt 2 \).
a) Tính theo a thể tích khối chóp \(S.ABCD.\)
b) Tính theo a khoảng cách giữa hai đường thẳng \(AD\) và \(SB\).

a) Gọi \(O\) là giao điểm của \(AC\) và \(BD\).
Vì \(S.ABCD\) là hình chóp đều nên \(SO \bot \left( {ABCD} \right)\).
Áp dụng định lý Pytago tính : \(SO = \sqrt {S{A^2} - O{A^2}} \).
Thể tích khối chóp \(S.ABCD\) bằng \(\frac{1}{3} \cdot {S_{ABCD}} \cdot SO\)
b) Vì \(AD//\left( {SBC} \right)\) và mặt phẳng \(\left( {SBC} \right)\) chứa \(SB\) nên
\(d\left( {AD,SB} \right) = d\left( {AD,\left( {SBC} \right)} \right) = d\left( {A,\left( {SBC} \right)} \right)\)
\(d\left( {A,\left( {SBC} \right)} \right) = 2.d\left( {O,\left( {SBC} \right)} \right)\).
Kẻ \(OM\) vuông góc với \(BC\) tại \(M,OH\) vuông góc với \(SM\) tại \(H\) thì
\(BC \bot \left( {SOM} \right) \Rightarrow BC \bot OH \Rightarrow OH \bot \left( {SBC} \right) \Rightarrow d\left( {O,\left( {SBC} \right)} \right) = OH.\)
Advertisements (Quảng cáo)
Tam giác \(SOM\)vuông tại \(O\), có đường cao \(OH\), khi đó \(OH = \frac{{SO \cdot OM}}{{SM}}\).
Suy ra \(d\left( {AD,SB} \right) = 2.OH\).

a) Gọi \(O\) là giao điểm của \(AC\) và \(BD\).
Vì \(S.ABCD\) là hình chóp đều nên \(SO \bot \left( {ABCD} \right)\).
Ta có tam giác \(SAO\) vuông tại \(O\) nên theo định lý Pythagore: \(SO = \sqrt {S{A^2} - O{A^2}} = \frac{{a\sqrt 6 }}{2}\).
Thể tích khối chóp \(S.ABCD\) bằng \(\frac{1}{3} \cdot {S_{ABCD}} \cdot SO = \frac{{{a^3}\sqrt 6 }}{6}.\)

b) Vì \(AD//\left( {SBC} \right)\) và mặt phẳng \(\left( {SBC} \right)\) chứa \(SB\) nên
\(d\left( {AD,SB} \right) = d\left( {AD,\left( {SBC} \right)} \right) = d\left( {A,\left( {SBC} \right)} \right)\)
Đường thẳng \(AO\) cắt mặt phẳng \(\left( {SBC} \right)\) tại \(C\) và \(O\) là trung điểm của đoạn \(AC\) nên \(d\left( {A,\left( {SBC} \right)} \right) = 2.d\left( {O,\left( {SBC} \right)} \right)\).
Kẻ \(OM\) vuông góc với \(BC\) tại \(M,OH\) vuông góc với \(SM\) tại \(H\) thì
\(BC \bot \left( {SOM} \right) \Rightarrow BC \bot OH \Rightarrow OH \bot \left( {SBC} \right) \Rightarrow d\left( {O,\left( {SBC} \right)} \right) = OH.\)
Tam giác \(SOM\)vuông tại \(O\), có đường cao \(OH\), khi đó \(OH = \frac{{SO \cdot OM}}{{SM}} = \frac{{a\sqrt {42} }}{{14}}\).
Vậy \(d\left( {AD,SB} \right) = 2.OH = \frac{{a\sqrt {42} }}{7}\).
