Cho tam giác ABC. Trong nửa mặt phẳng có bờ là đường thẳng BC không chứa điểm A, ta dựng hình vuông BCDE. Kẻ DM vuông góc với AB, EN vuông góc với AC, và kẻ đường cao AH của tam giác ABC. Chứng minh rằng ba đường thẳng AD, EN, và AH đồng quy.

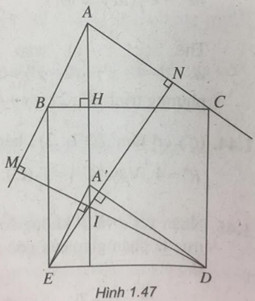
Nếu ta “ kéo “ tam giác ABC xuống theo phương AH sao cho B trùng E, C trùng D thì A trùng với A’. Khi đó MD, EN, AH là ba đường cao của tam giác A’ED nên chúng đồng quy.
Thực hiện phép tịnh tiến theo vectơ \(\overrightarrow {BE} \) ta có
\({T_{\overrightarrow {BE} }}:A \mapsto A’\)
\(B \mapsto E\)
\(C \mapsto D\)
Khi đó, ta có: \(A’E\parallel AB,A’D\parallel AC\).
Advertisements (Quảng cáo)
Gọi \(I = DM \cap EN\)
Ta có:
\(\left\{ \matrix{
AB \bot DM \hfill \cr
AB\parallel A’E \hfill \cr} \right. \Rightarrow DM \bot A’E\)
Tương tự, ta có: \(EN \bot A’D\).
Xét ∆A’ED, vì I là giao điểm của hai đường cao nên I là trực tâm của tam giác trên.
Suy ra \(A’I \bot E{\rm{D}}\)
\( \Rightarrow AI \bot BC’\) hay \(I \in AH\)
Vậy AH, DM, EN đồng quy tại I.
