Cho đường tròn (O, R) , gọi BC là dây cung cố định của đường tròn và A là một điểm di động trên đường tròn. Tìm tập hợp trực tâm H của tam giác ABC.

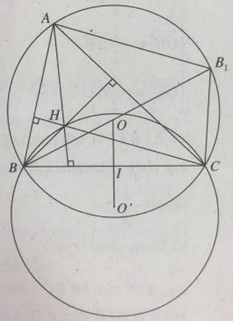
Vẽ đường kính BB1. Vì \(A{B_1}\parallel HC\) và \(AH\parallel {B_1}C\) nên AHCB1 là hình bình hành, suy ra: \(\overrightarrow {AH} = \overrightarrow {{B_1}C} \). B, C cố định nên \(\overrightarrow {{B_1}C} \) không đổi.
Như vậy \(H = {T_{\overrightarrow {{B_1}C} }}\left( A \right)\). Suy ra tập hợp các điểm H là đường tròn \(C’\left( {O’;R} \right)\), chính là ảnh của đường tròn \(C\left( {O;R} \right)\) qua phép tịnh tiến \({T_{\overrightarrow {{B_1}C} }}\).
Advertisements (Quảng cáo)
+ Xác định tâm của (C’):
Ta có:
\(O’ = {T_{\overrightarrow {{B_1}C} }}\left( O \right),\overrightarrow {OO’} = \overrightarrow {{B_1}C} = 2\overrightarrow {OI} \)
(I là trung điểm của BC). Vậy O’ đối xứng với O qua BC.
