Tìm chu vi của tam giác ABC.. Bài 1.52 trang 41 Sách bài tập (SBT) Hình học 11 - Đề toán tổng hợp Chương I
Cho tam giác đều ABC và điểm P nằm trong tam giác, sao cho PC = 3, PA = 4 và PB = 5. Tìm chu vi của tam giác ABC.
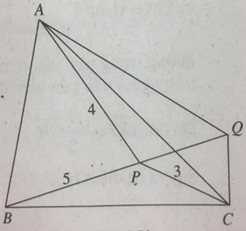
Xét phép quay \({Q_{\left( {C,{{60}^0}} \right)}}:\Delta CBP \mapsto \Delta CAQ\).
Ta có :
Advertisements (Quảng cáo)
\(\left\{ \matrix{
CP = CQ \hfill \cr
\widehat {PCQ} = {60^0} \hfill \cr} \right. \Rightarrow \Delta PCQ\) là tam giác đều.
\(\left\{ \matrix{
AQ = BP = 5 \hfill \cr
AP = 4 \hfill \cr
PQ = PC = 3 \hfill \cr} \right. \Rightarrow A{Q^2} = A{P^2} + P{Q^2}\)
\( \Rightarrow \widehat {APQ} = {90^0}\)
\(\widehat {APC} = \widehat {APQ} + \widehat {QPC} = {90^0} + {60^0} = {150^0}\)
Áp dụng định lí hàm số côsin trong tam giác APC ta tính được chu vi tam giác ABC là: \(p = 3{\rm{A}}C = 3\sqrt {25 + 12\sqrt 3 } \)