Cho hai đường tròn có cùng bán kính R cắt nhau tại hai điểm M, N. Bài 1.50 trang 41 Sách bài tập (SBT) Hình học 11 - Đề toán tổng hợp Chương I
Cho hai đường tròn có cùng bán kính R cắt nhau tại hai điểm M, N. Đường trung trực của MN cắt hai đường tròn tại hai điểm A, Bvà nằm cùng phía đối với MN. Chứng minh rằng \(M{N^2} + A{B^2} = 4{R^2}\).
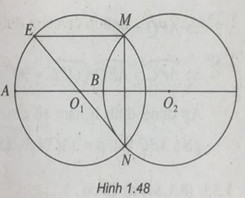
\({T_{\overrightarrow {{O_2}{O_1}} }}:B \mapsto A\)
Advertisements (Quảng cáo)
\(M \mapsto E\)
\( \Rightarrow \overrightarrow {BA} = \overrightarrow {ME} = \overrightarrow {{O_2}{O_1}} \)
∆NME vuông tại M (vì \(ME\parallel AB\) và \(AB \bot MN\)), do đó NE là đường kính. Từ đó ta có:
\(\eqalign{
& N{E^2} = N{M^2} + M{E^2} \cr
& \Leftrightarrow {\left( {2{\rm{R}}} \right)^2} = M{N^2} + A{B^2} \cr
& \Leftrightarrow M{N^2} + A{B^2} = 4{{\rm{R}}^2} \cr} \)