Cho tứ diện ABCD. Gọi G1 và G2 lần lượt là trọng tâm của tam giác ACD và BCD. Chứng minh rằng G1G2 song song với các mặt phẳng (ABC) và (ABD).. Bài 2.16 trang 74 Sách bài tập (SBT) Hình học 11 - Bài 3. Đường thẳng và mặt phẳng song song
Cho tứ diện ABCD. Gọi G1 và G2 lần lượt là trọng tâm của tam giác ACD và BCD. Chứng minh rằng G1G2 song song với các mặt phẳng (ABC) và (ABD).
(h.2.34)
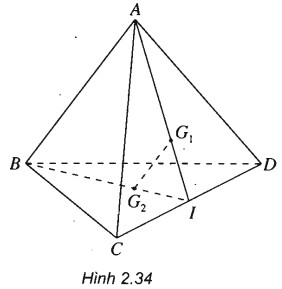
Gọi I là trung điểm của CD.
Vì G1 là trọng tâm của tam giác ACD nên \({G_1} \in AI\)
Advertisements (Quảng cáo)
Vì G2 là trọng tâm của tam giác BCD nên \({G_2} \in BI\)
Ta có :
\(\left\{ \matrix{
{{I{G_1}} \over {IA}} = {1 \over 3} \hfill \cr
{{I{G_2}} \over {IB}} = {1 \over 3} \hfill \cr} \right. \Rightarrow {{I{G_1}} \over {IA}} = {{I{G_2}} \over {IB}} \Rightarrow {G_1}{G_2}\parallel AB\)
\(AB \subset \left( {ABC} \right) \Rightarrow {G_1}{G_2}\parallel \left( {ABC} \right)\)
Và \(AB \subset \left( {ABD} \right) \Rightarrow {G_1}{G_2}\parallel \left( {ABD} \right)\)