Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt .Gọi O là giao điểm của AC và BD, O’ là giao điểm của AE và BF.
a) Chứng minh rằng OO’ song song với hai mặt phẳng (ADF) và (BCE)
b) Gọi M và N lần lượt là trọng tâm của các tam giác ABDvà ABE. Chứng minh rằng .

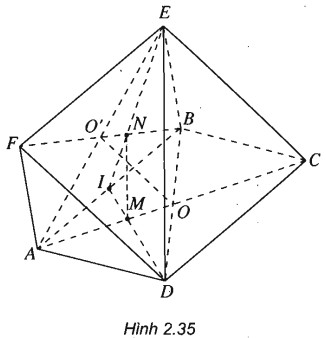
(h.2.35)
a) Ta có : \(OO’\parallel DF\) ( đường trung bình của tam giác BDF).
Vì \(DF \subset \left( {ADF} \right) \Rightarrow OO’\parallel \left( {ADF} \right)\).
Tương tự \(OO’\parallel EC\) (đường trung bình của tam giác AEC).
Vì \(EC \subset \left( {BCE} \right)\) nên \(OO’\parallel \left( {BCE} \right)\).
Advertisements (Quảng cáo)
b) Gọi I là trung điểm AB;
Vì M là trọng tâm của tam giác ABD nên \(M \in DI\)
Vì N là trọng tâm của tam giác ABE nên \(N \in EI\)
Ta có :
\(\left\{ \matrix{
{{IM} \over {I{\rm{D}}}} = {1 \over 3} \hfill \cr
{{IN} \over {IE}} = {1 \over 3} \hfill \cr} \right. \Rightarrow {{IM} \over {I{\rm{D}}}} = {{IN} \over {IE}} \Rightarrow MN\parallel DE\)
Mà
\(\left\{ \matrix{
C{\rm{D}}\parallel AB \hfill \cr
C{\rm{D}} = AB \hfill \cr
EF\parallel AB \hfill \cr
EF = AB \hfill \cr} \right.\)
Nên \(C{\rm{D}}\parallel EF\) và \(C{\rm{D = }}EF\), suy ra tứ giác CDFE là hình bình hành.
\(\left\{ \matrix{
MN\parallel DE \hfill \cr
DE \subset \left( {CEF} \right) \hfill \cr} \right. \Rightarrow MN\parallel \left( {CEF} \right)\)
