Bài 1.28 trang 11 Sách bài tập (SBT) Vật lí 11 nâng cao
Trong mặt phẳng tọa độ xOy có ba điện tích điểm (Hình 1.6).
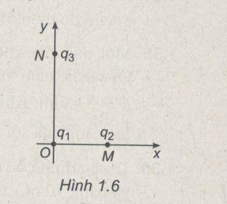
Điện tích \({q_1} = + 4\mu C\) được giữ tại gốc tọa độ O. Điện tích \({q_2} = - 3\mu C\) đặt cố định tại M trên trục Ox, \(\overline {OM} = + 5cm\). Điện tích \({q_3} = - 6\mu C\) đặt cố định tại N trên trục Oy, \(\overline {ON} = + 10cm\). Bỏ lực giữ để điện tích \({q_1}\) chuyển động. Hỏi ngay sau khi được giải phóng thì điện tích \({q_1}\) có gia tốc bằng bao nhiêu ? Vẽ vecto gia tốc của \({q_1}\) lúc đó . Cho biết hạt mang điện tích \({q_1}\) có khối lượng \(m = 5g\).

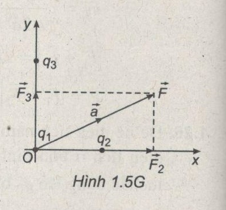
Gọi \(\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) là các lực mà \({q_2},{q_3}\) tác dụng lên \({q_1}\) (Hình 1.5G)
Advertisements (Quảng cáo)
\({F_2} = k{{\left| {{q_1}{q_2}} \right|} \over {r_2^2}};{F_3} = k{{\left| {{q_1}{q_3}} \right|} \over {r_3^2}}\)
\({{{F_2}} \over {{F_3}}} = {{{q_2}} \over {{q_3}}}{\left( {{{{r_3}} \over {{r_2}}}} \right)^2} = 2\)
\({F^2} = F_2^2 + F_3^2 = 5F_3^2\)
\(F = ma\)
Suy ra \(a = {F \over m} = {{\sqrt 5 {F_3}} \over m} = {{9.24} \over {\sqrt 5 }}{10^2} = 9660m/{s^2}.\)
