Advertisements (Quảng cáo)
Bài 2.25 trang 24 Sách bài tập (SBT) Vật lí 11 nâng cao
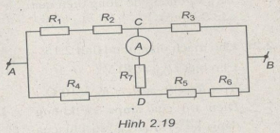
Cho mạch điện có dạng như Hình 2.19. Cho biết \({R_1} = {R_4} = {R_6} = 1\Omega ;{R_2} = {R_5} = 3\Omega ;\) \({R_7} = 4\Omega ;{R_3} = 16\Omega .\)
a, Tính \({R_{AB}}.\)
b, Cho \({U_{AB}} = 4V.\) Tìm cường độ dòng điện qua các điện trở và số chỉ ampe kế.
a, Ta có:
\(\eqalign{
& {R_{12}} = {R_1} + {R_2} = 4\Omega \cr
& {R_{56}} = {R_5} + {R_6} = 4\Omega \cr} \)
Ta nhận xét rằng :
\({{{R_{12}}} \over {{R_4}}} = {4 \over 1};{{{R_3}} \over {{R_{56}}}} = {{16} \over 4}\)
Vậy ta có : \({{{R_{12}}} \over {{R_4}}} = {{{R_3}} \over {{R_{56}}}}\); mạch cầu cân bằng.
Từ đó, \({I_7} = 0\) và \({V_C} = {V_D},\) nghĩa là có thể chập hai điểm C và D lại khi tính điện trở và cường độ dòng điện qua các điện trở. Khi đó, các điện trở trong mạch được mắc như sau :
\(\left( {{R_{12}}//{R_4}} \right)nt\left( {{R_3}//{R_{56}}} \right).\)
Advertisements (Quảng cáo)
Do đó:
\(\eqalign{
& {R_{124}} = {{{R_{12}}{R_4}} \over {{R_{12}} + {R_4}}} = 0,8\Omega \cr
& {R_{356}} = {{{R_3}{R_{56}}} \over {{R_3} + {R_{56}}}} = 3,2\Omega \cr} \)
Và \({R_{AB}} = {R_{124}} + {R_{356}} = 4\Omega .\)
b, \({I_{AB}} = {{{U_{AB}}} \over {{R_{AB}}}} = 1A\) \( \Rightarrow {U_{AC}} = {I_{AB}}{R_{124}} = 0,8V\)
Từ đó: \({I_1} = {I_2} = {{{U_{AC}}} \over {{R_{12}}}} = 0,2A;\) \(\,{I_4} = {{{U_{AC}}} \over {{R_4}}} = 0,8A.\)
Ta lại có: \({U_{CB}} = {I_{AB}}{R_{356}} = 3,2V\)
Từ đó: \({I_3} = {{{U_{CB}}} \over {{R_3}}} = 0,2A;\) \({I_5} = {I_6} = {{{U_{CB}}} \over {{R_{56}}}} = 0,8A.\)
Vì mạch cầu cân bằng nên cũng có thể kết luận ngay là :
\(\eqalign{
& {I_3} = {I_1} = {I_2} = 0,2A \cr
& {I_5} = {I_6} = {I_4} = 0,8A \cr} \)
Ampe kế chỉ số 0.