Advertisements (Quảng cáo)
Bài 7.29 trang 85 Sách bài tập (SBT) Vật lí 11 nâng cao
Một chậu thủy tinh nằm ngang chứa một lớp nước dày có chiết suất \({4 \over 3}\).
Một tia sáng SI chiết tới mặt nước với góc tới là \({45^o}\).
a) Tính góc lệch \({D_1}\) giữa tia khúc xạ và tia tới.
b) Bỏ qua bề dày của đáy chậu. Tính góc ló của tia sáng đi ra khỏi đáy chậu và góc lệch D của tia ló này với tia tới SI.
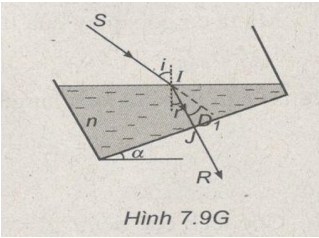
c) Giữ phương tia tới không đổi. Nghiêng đáy chậu một góc đối với mặt ngang. Hỏi giá trị của \(\alpha \) để góc lệch làm bởi tia sáng ló ra khỏi đáy chậu với tia tới SI cũng là \({D_1}\)?
a) Ta có: \(\sin r = {{\sin i} \over n}\) với \(i = {45^o},n = {4 \over 3}\)
\(\eqalign{
& \sin r = 0,5302 \cr
& \Rightarrow r = {32^o} \cr} \)
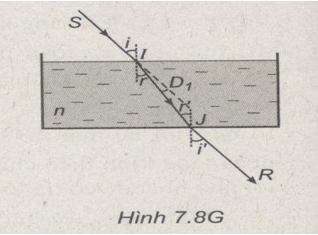
Suy ra: \({D_1} = i – r = {13^o}\) (Hình 7.8G).
Advertisements (Quảng cáo)
b) Góc tới tại J là r.
\(\sin i’ = n\sin r = \sin i \Rightarrow i’ = i\)
Do đó, tia ló JR song song với tia tới SI hay góc lệch D = 0.
c) Góc lệch giữa tia ló và tia tới bây giờ là :
\(D = {D_1} \pm {D_2}\)
Trong đó: \({D_2}\) là góc lệch tại J khi đáy chậu nghiêng một góc \(\alpha \). Ta lấy dấu (+) nếu các độ lệch \({D_1}\) và \({D_2}\) cùng chiều ; lấy dấu (-) nếu hai góc lệch này ngược chiều.
Muốn \(D = {D_1}\) ta phải có \({D_2} = 0\). Muốn vậy, ti IJ phải vuông góc với đáy chậu.
Vậy phải nghiêng chậu một góc \(\alpha = r = {32^o}\) (Hình 7.9G).
