Bài 7.33 trang 86 Sách bài tập (SBT) Vật lí 11 nâng cao
Thấu kính hội tụ \({L_1}\) có tiêu cự 50 cm. Thấu kính phân kì \({L_2}\) có tiêu cự 30 cm. Hai thấu kính được ghép đồng trục.
a) Một vật thẳng AB được đặt vuông góc với quang trục của hệ, cách \({L_1}\) 30 cm. Chùm sáng từ vật qua \({L_1}\) rồi qua \({L_2}\). Hai thấu kính cách nhau 30 cm. Tìm vị trí và số phóng đại của ảnh.
b) Bây giờ đặt \({L_2}\) cách \({L_1}\) một khoảng \(\alpha \). Hỏi a bằng bao nhiêu thì độ lớn của ảnh cuối cùng không thay đổi khi ta di chuyển vật lại gần hệ thấu kính ?

a) Sơ đồ tạo ảnh :
\(A{B_{{d_1}}}{\buildrel {\left( {{L_1}} \right)} \over
\longrightarrow _{d{‘_1}}}{A_1}{B_1}_{{d_2}}{\buildrel {\left( {{L_2}} \right)} \over
\longrightarrow _{d{‘_2}}}{A_2}{B_2}\)
Khoảng cách từ \({A_1}{B_1}\) tới \({L_1}\):
\(d{‘_1} = {{{d_1}{f_1}} \over {{d_1} - {f_1}}}\) với \({d_1} = 30cm,{f_1} = 50cm\).
\(d{‘_1} = - 75cm\)
\({A_1}{B_1}\) cách \({L_2}\) là: \(d_2 = a - d{‘_1} = 30 + 75 = 105cm\); \({A_1}{B_1}\) là vật đối với \({L_2}\), cho ảnh là \({A_2}{B_2}\) cách \({L_2}\) là:
\(d{‘_2} = {{{d_2}{f_2}} \over {{d_2} - {f_2}}}\) với \({f_2} = - 30cm\)
\(d{‘_2} = - 23,3cm\): ảnh \({A_2}{B_2}\) là ảnh ảo.
Số phóng đại \(k = {{\overline {{A_2}{B_2}} } \over {\overline {AB} }} = {k_1}{k_2} = {{d{‘_1}} \over {{d_1}}}.{{d{‘_2}} \over {{d_2}}} \approx 0,6\)
Vậy ảnh \(A_2B_2\) cùng chiều với AB và có độ lớn là \(A_2B_2=0,6AB\).
b) Bây giờ \({d_1}\) là biến số, a là thông số phải xác định trị số.
Ta có : \(d{‘_1} = {{{d_1}{f_1}} \over {{d_1} - {f_1}}}\)
Advertisements (Quảng cáo)
Suy ra : \({d_2} = a - d{‘_1} = a - {{{d_1}{f_1}} \over {{d_1} - {f_1}}}\) và \(d{‘_2} = {{{d_2}{f_2}} \over {{d_2} - {f_2}}}\)
Số phóng đại :
\(\eqalign{
& k = {{\overline {{A_2}{B_2}} } \over {\overline {AB} }} \cr&= {{d{‘_1}} \over {{d_1}}}.{{d{‘_2}} \over {{d_2}}} = {{{f_1}} \over {{d_1} - {f_1}}}.{{{f_2}} \over {{d_2} - {f_2}}} \cr
& k = {{{f_1}} \over {{d_1} - {f_1}}}{{{f_2}} \over {a - {{{d_1}{f_1}} \over {{d_1} - {f_1}}} - {f_2}}} \cr
& = {{{f_1}{f_2}} \over {a\left( {{d_1} - {f_1}} \right) - {d_1}{f_1} - {f_2}\left( {{d_1} - {f_1}} \right)}} \cr
& k = {{{f_1}{f_2}} \over {\left( {a - {f_1} - {f_2}} \right){d_1} + {f_1}\left( { - a + {f_2}} \right)}} \cr} \)
Muốn độ lớn của ảnh \({A_2}{B_2}\) không đổi khi ta di chuyển vật lại gần thấu kính, số phóng đại k phải độc lập với \({d_1}\).
Muốn vậy, ta phải có : \(a - {f_1} - {f_2} = 0\)
Hay: \(a = {f_1} + {f_2} = 20cm\).
- Ta có thể giải câu b một cách đơn giản hơn. Quan sát đường đi tia sáng trình bày ở Hình 7.13G :
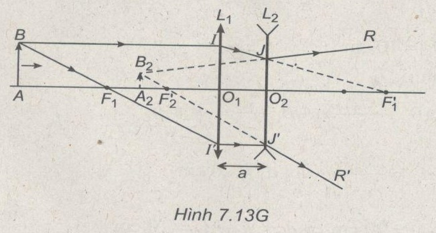
Khi cho vật AB tiến lại gần hệ thấu kính, đường đi tia sáng BIJR không đổi, trong khi BI’ quay xung quanh tiêu điểm \({F_1}\), đoạn I’J’ hạ thấp xuống, tia J’R’ quay quanh tiêu điểm ảnh \(F{‘_2}\) của \({L_2}\).
Ảnh \({B_2}\) là điểm cắt nhau của hai tia ló JR và J’R’ nên \({B_2}\) chạy trên giá của tia JR. Vậy trong trường hợp tổng quát, độ lớn của \({A_2}{B_2}\) thay đổi khi cho vật AB tiến lại gần \({L_1}\).
Muốn độ lớn của \({A_2}{B_2}\) không đổi, tia ló JR phải song song với trục của hệ thấu kính. Muốn vậy, tia IJ phải có giá đi qua tiêu điểm vật \({F_2}\) của \({L_2}\).
Suy ra, ta phải có \({F_2} \equiv F{‘_1}\)
Hay \(a = {O_1}{O_2} = {O_1}F{‘_1} - {O_2}{F_2}\)
\(a = 20cm\)
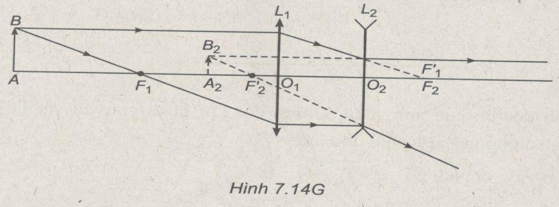
Đường đi tia sáng như trong Hình 7.14G