Bài 7.39 trang 88 Sách bài tập (SBT) Vật lí 11 nâng cao
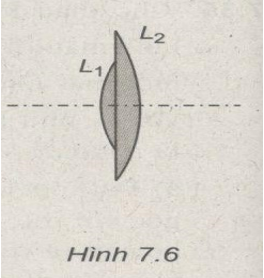
Hai thấu kính cùng có một mặt phẳng và một mặt lồi có bán kính R = 15 cm, chiết suất n = 1,5 nhưng đường kính khẩu độ khác nhau, được ghép đồng trục với nhau như Hình 7.6.
a) Đặt một vật nhỏ AB vuông góc với quang trục của hệ và cách hệ một đoạn d. Chứng tỏ rằng hệ thấu kính sẽ cho hai ảnh phân biệt.
b) Tìm điều kiện về d để hai ảnh trên cùng thật hay cùng ảo.
Chứng tỏ rằng nếu hai ảnh cùng ảo hay cùng thật thì độ lớn của chúng không thể bằng nhau.
c) Tìm d để hai ảnh trên có độ lớn bằng nhau. Tính số phóng đại của chúng.

a) Tiêu cự của các thấu kính :
\({1 \over {{f_1}}} = {1 \over {{f_2}}} = \left( {n - 1} \right)\left( {{1 \over {{R_1}}} + {1 \over {{R_2}}}} \right)\)
Với \(n = 1,5;{R_1} = \infty ,{R_2} = 15cm\)
Suy ra: \({f_1} = {f_2} = {{{R_2}} \over {n - 1}} = 30cm\)
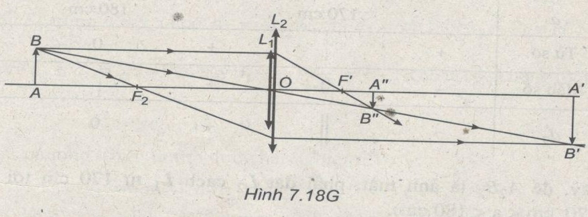
Xét một chùm sáng từ B tới hệ thấu kính. Phần ngoài của chùm sáng chỉ đi qua \({L_2}\), cho ảnh là A’B’. Phần trong của chùm sáng đi qua thấu kính ghép \(\left( {{L_1} + {L_2}} \right)\) cho ảnh A”B”. Đây là hai ảnh phân biệt (Hình 7.18G).
b) Các sơ đồ tạo ảnh như sau :
\(A{B_d}{\buildrel {\left( {{L_2}} \right)} \over
\longrightarrow _{d’}}A’B’\)
Và \(A{B_d}{\buildrel {\left( {{L_1} + {L_2}} \right)} \over
\longrightarrow _{d’}}A”B”\)
Ta có: \(d’ = {{d{f_2}} \over {d - {f_2}}}\)
Và \(d” = {{df} \over {d - f}}\) với \({1 \over f} = {1 \over {{f_1}}} + {1 \over {{f_2}}}\).
Muốn hai ảnh A’B’ và A”B” cùng thật thì khoảng cách từ AB đến quang tâm chung của hai thấu kính phải lớn hơn \({f_2}\) (hay f) nếu \({f_2} > f\) (nếu \({f_2} < f\)).
\(f = {{{f_1}{f_2}} \over {{f_1} + {f_2}}} = 15cm < {f_2} = 30cm\)
Vậy \(d > 30cm\).
Advertisements (Quảng cáo)
Muốn hai ảnh trên cùng ảo thì khoảng cách từ AB đến quang tâm phải nhỏ hơn \({f_2}\) (hay f) nếu \({f_2} < f\) (nếu \({f_2} > f\)).
Suy ra: \(d < 15cm\).
Nhận xét :
- Nếu hai ảnh cùng thật thì cùng ngược chiều với vật.
-Nếu hai ảnh cùng ảo thì đều cùng chiều với vật.
Vậy, trong cả hai trường hợp trên, hai ảnh A’B’ và A”B” đều cùng chiều với nhau.
- Số phóng đại của A’B’: \(k = - {{d’} \over d}\)
- Số phóng đại của A”B”: \(k’ = - {{d”} \over d}\) cùng dấu với k.
Ta có: \({{k’} \over k} = {{d”} \over {d’}} \ne 1\)
Vậy, trong hai trường hợp trên, độ lớn của hai ảnh phải khác nhau.
c) Để hai ảnh trên có độ lớn bằng nhau thì phải có một ảnh ảo và một ảnh thật. Trong trường hợp này, ta phải có \(f < d < {f_2}\) hay \(15cm < d < 30cm\).
Suy ra hai ảnh A’B’ và A”B” ngược chiều nhau :
\({{k’} \over k} = - 1\) hay \(k’ = - k\)
\( \Rightarrow - {{d”} \over d} = {{d’} \over d}\) hay \( - d” = d’\)
\( - {{df} \over {d - f}} = {{d{f_2}} \over {d - {f_2}}}\)
Hay \( - {{15} \over {d - 15}} = {{30} \over {d - 30}}\)
Suy ra: d = 20cm
Các số phóng đại của các ảnh là :
\(\eqalign{
& k = - {{d’} \over d} = - {{{f_2}} \over {d - {f_2}}} = 3 \cr
& k’ = - {{d”} \over d} = - {f \over {d - f}} = - 3 \cr} \)
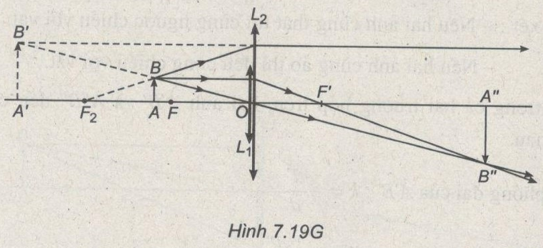
- Đường đi tia sáng (Hình 7.19G) :