Dựa vào các hệ số và tính đồng biến, nghịch biến của hàm số mũ để suy ra . Hướng dẫn cách giải/trả lời bài 13 trang 56 SGK Toán 11 tập 2 - Cánh Diều Bài tập cuối chương VI. Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ (y = {a^x};, y = {b^x}...Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ \(y =

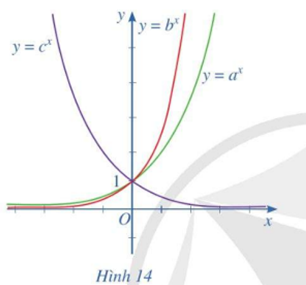
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số mũ \(y = {a^x};\,y = {b^x};\,y = {c^x}\) được cho bởi Hình 14. Kết luận nào sau đây là đúng đối với ba số a, b, c ?
A. c < a < b
B. c < b < a
C. a < b < c
Advertisements (Quảng cáo)
D. b < c < a

Dựa vào các hệ số và tính đồng biến, nghịch biến của hàm số mũ để suy ra

- Do \({c^x}\) nghịch biến, \({a^x},{b^x}\) đồng biến => c < 1, a > 1, b > 1 => c nhỏ nhất => loại C, D
- Dựa vào đồ thị ta thấy, \({b^x}\) có đồ thị đi lên cao hơn so với \({a^x}\) => b > a => Chọn A
