Các hàm đa thức liên tục trên \(\mathbb{R}\) . Giải và trình bày phương pháp giải bài 6 trang 77 SGK Toán 11 tập 1 - Cánh Diều Bài 3. Hàm số liên tục. Hình 16 biểu thị độ cao h (m) của một quả bóng được đá lên theo thời gian t (s), trong đó \(h\left( t \right) = - 2{t^2} + 8t...

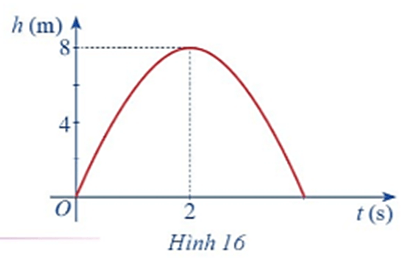
Hình 16 biểu thị độ cao h (m) của một quả bóng được đá lên theo thời gian t (s), trong đó \(h\left( t \right) = - 2{t^2} + 8t.\)
a) Chứng tỏ hàm số \(h\left( t \right)\) liên tục trên tập xác định.
b) Dựa vào đồ thị hãy xác định \(\mathop {\lim }\limits_{t \to 2} \left( { - 2{t^2} + 8t} \right).\)
Advertisements (Quảng cáo)

Các hàm đa thức liên tục trên \(\mathbb{R}\)

a) Hàm số \(h\left( t \right) = - 2{t^2} + 8t\) là hàm đa thức nên liên tục trên \(\mathbb{R}\) do đó hàm số \(h\left( t \right)\) liên tục trên tập xác định.
b) Dựa vào đồ thị hàm số khi t tiến dần đến 2 thì h(t) dần đến 8.
Vậy \(\mathop {\lim }\limits_{t \to 2} \left( { - 2{t^2} + 8t} \right) = 8\)
