Hoạt động 1
Trong bài toán ở phần mở đầu, giả sử r = 1,14%/năm
a) Viết phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lũy thừa?

Dựa vào công thức đã tìm được ở bài mở đầu rồi tính

a) Phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu là:
\(S = 2S.{e^{1,14.t}} \Leftrightarrow 2{e^{1,14t}} = 1 \Leftrightarrow {e^{1,14t}} = \frac{1}{2}\)
b) Phương trình vừa tìm được có ẩn là t và nằm ở vị trí mũ của lũy thừa
Luyện tập – Vận dụng 1
Cho hai ví dụ về phương trình mũ

Dựa vào kiến thức vừa học để xác định phương trình mũ

2 ví dụ về phương trình mũ
Hoạt động 2
a) Vẽ đồ thị hàm số \(y = {3^x}\) và đường thẳng y = 7
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình \({3^x} = 7\)

Dựa vào kiến thức đã học ở bài trước để vẽ đồ thị

a) Ta có bảng sau:

Ta có đồ thị sau:
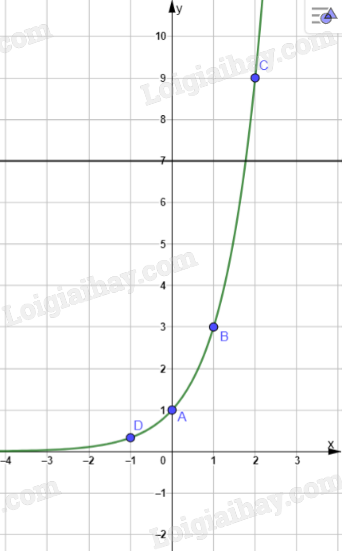
b, Hai đồ thị \(y = {3^x}\) và y = 7 có 1 giao điểm. Vậy số nghiệm của phương trình \({3^x} = 7\) là 1
Luyện tập – Vận dụng 2
Giải mỗi phương trình sau:
a) \({9^{16 - x}} = {27^{x + 4}}\)
b) \({16^{x - 2}} = 0,{25.2^{ - x + 4}}\)

Dựa vào kiến thức vừa học về phương trình mũ để giải

a) \({9^{16 - x}} = {27^{x + 4}}\)
\(\begin{array}{l} \Leftrightarrow {3^{2.\left( {16 - x} \right)}} = {3^{3.\left( {x + 4} \right)}}\\ \Leftrightarrow 2.\left( {16 - x} \right) = 3.\left( {x + 4} \right)\\ \Leftrightarrow 32 - 2x - 3x - 12 = 0\\ \Leftrightarrow - 5x = - 20\\ \Leftrightarrow x = 4\end{array}\)
b) \({16^{x - 2}} = 0,{25.2^{ - x + 4}}\)
Advertisements (Quảng cáo)
\(\begin{array}{l} \Leftrightarrow {2^{4\left( {x - 2} \right)}} = 0,{25.2^{ - x + 4}}\\ \Leftrightarrow {2^{4x - 8 + x - 4}} = 0,25\\ \Leftrightarrow {2^{5x - 12}} = 0,25\\ \Leftrightarrow 5x - 12 = {\log _2}0,25\\ \Leftrightarrow 5x - 12 = - 2\\ \Leftrightarrow x = 2\end{array}\)
Hoạt động 3
Chỉ số hay độ pH của một dung dịch được tính theo công thức: \(pH = - \log [{H^ + }]\) (Trong đó \([{H^ + }]\) chỉ nống độ hydrogen). Đo chỉ số pH của một mẫu nước sông, ta có kết quả là pH = 6,1.
a) Viết phương trình thể hiện nồng độ x của ion hydrogen \([{H^ + }]\) trong mẫu nước sông đó.
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lôgarit?

Dựa vào công thức tính pH để biểu diễn

a) Ta có: \( - \log [{H^ + }] = 6.1 \Leftrightarrow - \log x = 6,1\)
b) Phương trình vừa tìm được có ẩn là x và nằm ở vị trí hệ số của logarit
Luyện tập – Vận dụng 3
Cho hai ví dụ về phương trình logarit

Dựa vào dạng phương trình logarit vừa học để làm

Hoạt động 4
a) Vẽ đồ thị hàm số \(y = {\log _4}x\) và đường thẳng y = 5
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình \({\log _4}x = 5\)

Dựa vào cách vẽ đồ thị ở bài trên để vẽ hàm

a) Đồ thị hai hàm số:
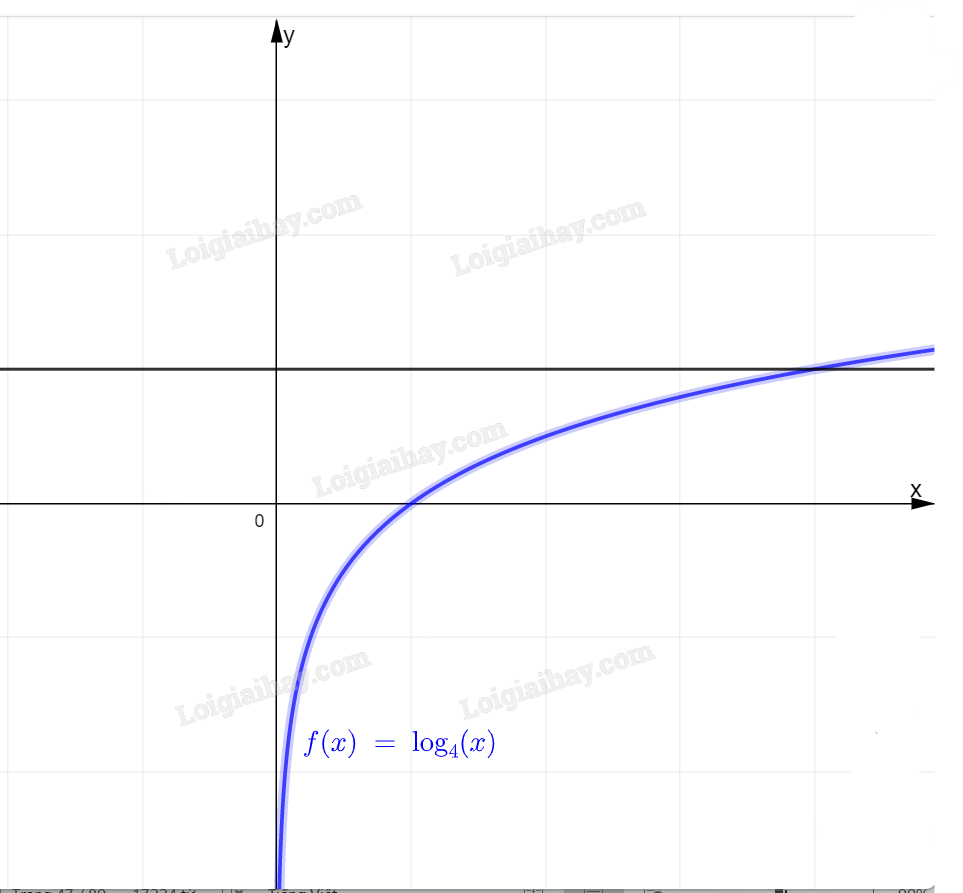
b, Hai hàm số có 1 giao điểm. Phương trình \({\log _4}x = 5\) có 1 nghiệm
Luyện tập – Vận dụng 4
Giải mỗi phương trình sau:
a) \({\log _5}\left( {2x - 4} \right) + {\log _{\frac{1}{5}}}\left( {x - 1} \right) = 0\)
b) \({\log _2}x + {\log _4}x = 3\)

Dựa vào công thức vừa học để giải phương trình

a) \({\log _5}\left( {2x - 4} \right) + {\log _{\frac{1}{5}}}\left( {x - 1} \right) = 0\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x > 2\\{\log _5}\left( {2x - 4} \right) - {\log _5}\left( {x - 1} \right) = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > 2\\{\log _5}\left( {\frac{{2x - 4}}{{x - 1}}} \right) = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > 2\\\frac{{2x - 4}}{{x - 1}} = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > 2\\2x - 4 = x - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > 2\\x = 3\end{array} \right.\\ \Leftrightarrow x = 3\end{array}\)
Vậy phương trình có nghiệm x = 3
b) \({\log _2}x + {\log _4}x = 3\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x > 0\\{\log _2}x + {\log _2}{x^2} = 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > 0\\{\log _2}{x^3} = 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > 0\\{x^3} = {2^3}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x = 2\end{array} \right.\\ \Leftrightarrow x = 2\end{array}\)
Vậy phương trình có nghiệm x = 2
