Bài 11 trang 87 Toán 11 tập 2 – Chân trời sáng tạo: Cho hình chóp $S. ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $D$; \(AB = AD =...

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $D$; $AB = AD = 2a;CD = a$; số đo góc nhị diện $\left[ {S,BC,A} \right]$ bằng ${60^ \circ }$. Gọi $I$ là trung điểm của cạnh $A{\rm{D}}$. Biết hai mặt phẳng $\left( {SBI} \right)$ và $\left( {SCD} \right)$ cùng vuông góc với mặt phẳng $\left( {ABCD} \right)$. Tính thể tích khối chóp $S.ABCD$ theo $a$.

Sử dụng công thức tính thể tích khối chóp: $V = \frac{1}{3}Sh$.

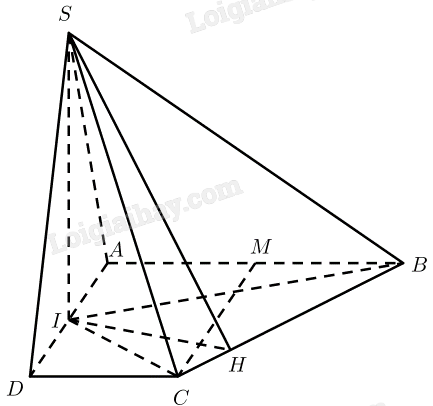
$\left. \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right\} \Rightarrow SI \bot \left( {ABCD} \right)$

Kẻ $IH \bot BC\left( {H \in BC} \right)$

$SI \bot \left( {ABCD} \right) \Rightarrow SI \bot BC$

$\Rightarrow BC \bot \left( {SIH} \right) \Rightarrow BC \bot SH$

Vậy $\widehat {AHI}$ là góc nhị diện $\left[ {S,BC,A} \right]$$\Rightarrow \widehat {AHI} = {60^ \circ }$

$\begin{array}{l}{S_{ABC{\rm{D}}}} = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).A{\rm{D}} = 3{a^2}\\AI = I{\rm{D}} = \frac{1}{2}A{\rm{D}} = a\\{S_{AIB}} = \frac{1}{2}AB.AI = {a^2},{S_{CI{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.I{\rm{D}} = \frac{{{a^2}}}{2}\\ \Rightarrow {S_{BIC}} = {S_{ABC{\rm{D}}}} - {S_{AIB}} - {S_{CI{\rm{D}}}} = \frac{{3{a^2}}}{2}\end{array}$

Gọi $M$ là trung điểm của $AB$

$\begin{array}{l} \Rightarrow BM = \frac{1}{2}AB = a,CM = AD = 2a \Rightarrow BC = \sqrt {B{M^2} + C{M^2}} = a\sqrt 5 \\ \Rightarrow IH = \frac{{2{{\rm{S}}_{BIC}}}}{{BC}} = \frac{{3a\sqrt 5 }}{5} \Rightarrow SI = IH.\tan \widehat {SHI} = \frac{{3a\sqrt {15} }}{5}\end{array}$

${V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SI = \frac{{3{a^3}\sqrt {15} }}{5}$