
Một chân cột bằng gang có dạng hình chóp cụt tứ giác đều có cạnh đáy lớn bằng \(2a\), cạnh đáy nhỏ bằng \(a\), chiều cao \(h = 2a\) và bán kính đáy phần trụ rỗng bên trong bằng \(\frac{a}{2}\).
a) Tìm góc phẳng nhị diện tạo bởi mặt bên và mặt đáy.
b) Tính thể tích chân cột nói trên theo \(a\).

‒ Cách xác định góc phẳng nhị diện \(\left[ {A,d,B} \right]\): Dựng mặt phẳng \(\left( P \right)\) vuông góc với \(d\), gọi \(a,a’\) lần lượt là giao tuyến của \(\left( P \right)\) với hai nửa mặt phẳng chứa \(A,B\), khi đó \(\left[ {A,d,B} \right] = \left( {a,a’} \right)\).
‒ Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS’} + S’} \right)\).
‒ Sử dụng công thức tính thể tích khối trụ: \(V = \pi {R^2}h\).

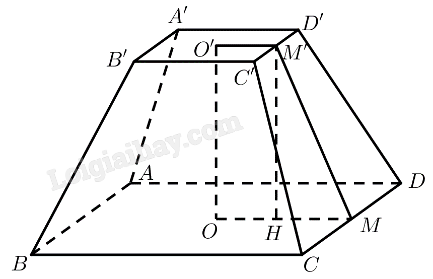
Mô hình hoá chân cột bằng gang bằng cụt chóp tứ giác đều \(ABCD.A’B’C’D’\) với \(O,O’\) là tâm của hai đáy. Vậy \(AB = 2{\rm{a}},A’B’ = a,OO’ = 2a\).
Gọi \(M,M’\) lần lượt là trung điểm của \(CD,C’D’\).
Advertisements (Quảng cáo)
\(A’B’C'{\rm{D}}’\) là hình vuông \( \Rightarrow O’M’ \bot C'{\rm{D}}’\)
\(CDD’C’\) là hình thang cân \( \Rightarrow MM’ \bot C’D’\)
Vậy \(\widehat {MM’O’}\) là góc phẳng nhị diện giữa mặt bên và đáy nhỏ, \(\widehat {M’MO}\) là góc phẳng nhị diện giữa mặt bên và đáy lớn.
Kẻ \(M’H \bot OM\left( {H \in OM} \right)\)
\(OMM’O’\) là hình chữ nhật
\( \Rightarrow OH = O’M’ = \frac{a}{2},OM = a,MH = OM - OH = \frac{{\rm{a}}}{2}\)
\(\begin{array}{l}\tan \widehat {M’MO} = \frac{{M’H}}{{MH}} = 4\\ \Rightarrow \widehat {M’MO} = 75,{96^ \circ } \Rightarrow \widehat {MM’O’} = {180^ \circ } - \widehat {M’MO} = 104,{04^ \circ }\end{array}\)
b) Diện tích đáy lớn là: \(S = A{B^2} = 4{{\rm{a}}^2}\)
Diện tích đáy bé là: \(S’ = A’B{‘^2} = {a^2}\)
Thể tích hình chóp cụt là: \({V_1} = \frac{1}{3}h\left( {S + \sqrt {SS’} + S’} \right) = \frac{1}{3}.2a\left( {4{{\rm{a}}^2} + \sqrt {4{{\rm{a}}^2}.{a^2}} + {a^2}} \right) = \frac{{14{{\rm{a}}^3}}}{3}\)
Thể tích hình trụ rỗng là: \({V_2} = \pi {R^2}h = \pi .{\left( {\frac{a}{2}} \right)^2}.2{\rm{a}} = \frac{{\pi {a^3}}}{2}\)
Thể tích chân cột là: \(V = {V_1} - {V_2} = \left( {\frac{{14}}{3} - \frac{\pi }{2}} \right){a^3}\).
